[Func-Num] 8.6 Graphs of Sin and Cos
Categories: Func-Num
📋 This is my note-taking from what I learned in the class “Math175-002 Functions & Number Systems”
Graphs of “y = a sin(bx + c)” and “y = a cos(bx + c)”
-
- Amplitude
- ymax = |a|
- ymin = -|a|
-
- Period → P = 2π/b
- P/4 = step on x-axis (five x values needed on x-axis to have graph for one period)
-
- Shift or Displacement = -c/b
- -c/b = Starting x value (c is called phase angle)
Note: You must have your Calculator on Radians
Example
Example 1: Sketching graph of “y = a sin(bx + c)”
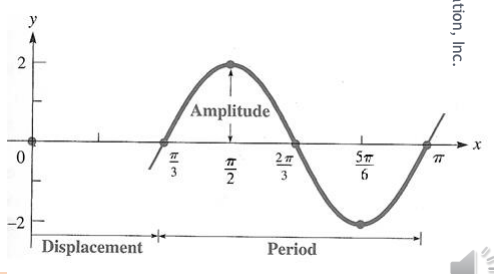
Sketch the graph y = 2 sin(3x - π).
| Solution | |
|---|---|
| a = 2 | Amplitude = ymax = |a| = 2, ymin = -|a| = -2 |
| b = 3 | Period(cycle) = P = 2π/b = 2π/3, P/4 = 2π/12 = π/6 = Step on x-axis |
| c = -π | Shift(Displacement) = -c/b = -(-π)/3 = π/3 = Starting x value on x-axis |
| x starts at π/3 and have five values on x-axis at a step = π/6 |
Sample Calculation: Calculator on Radians
- x = π/3 → y = 2 sin(3(π/3)-π) = 0
| x | \({π} \over {3}\) | \({π} \over {2}\) | \({2π} \over {3}\) | \({5π} \over {6}\) | π |
|---|---|---|---|---|---|
| y | 0 | 2 | 0 | -2 | 0 |
Example 2: Sketching graph of “y = a cos(bx + c)”
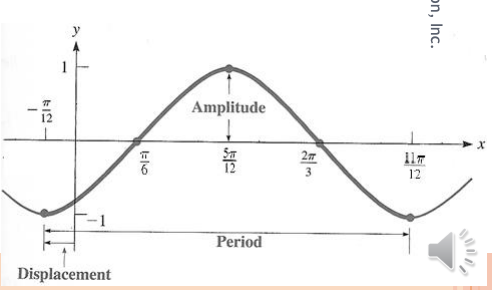
Sketch the graph y = -cos(2x + π/6).
| Solution | |
|---|---|
| a = -1 | Amplitude = ymax = |a| = 1, ymin = -|a| = -1 |
| b = 2 | Period(cycle) = P = 2π/b = 2π/2 = π, P/4 = π/4 = Step on x-axis |
| c = π/6 | Shift(Displacement) = -c/b = -(π/6)/2 = -π/12 = Starting x value on x-axis |
| x starts at -π/12 and have five values on x-axis at a step = π/4 |
Sample Calculation: Calculator on Radians
- x = -π/12 → y = -cos(2(-π/12) + π/6) = -1
| x | \({-π} \over {12}\) | \({π} \over {6}\) | \({5π} \over {12}\) | \({2π} \over {3}\) | \({11π} \over {12}\) |
|---|---|---|---|---|---|
| y | -1 | 0 | 1 | 0 | -1 |
Exercise
Exercise 1
For the function below:
- a) What is amplitude , ymax and ymin.
- b) What is the period?
- c) What is the shift (horizontal)?
- d) Graph one period and show values at 1/4th of the period, the shift and the amplitude.
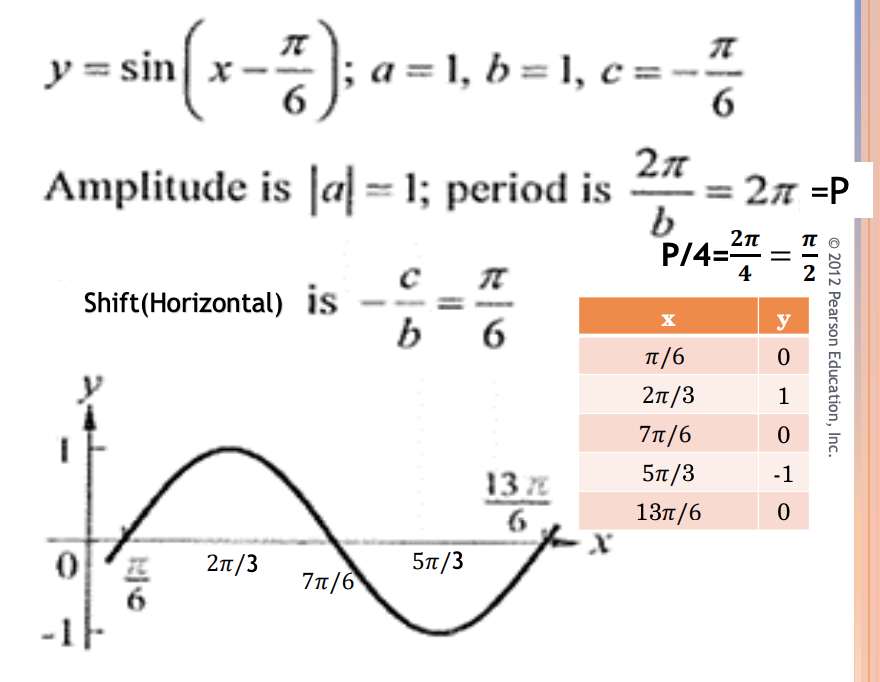
y = sin(x - π/6)
Exercise 2
For the function below:
- a) What is amplitude , ymax and ymin.
- b) What is the period?
- c) What is the shift (horizontal)?
- d) Graph one period and show values at 1/4th of the period, the shift and the amplitude.
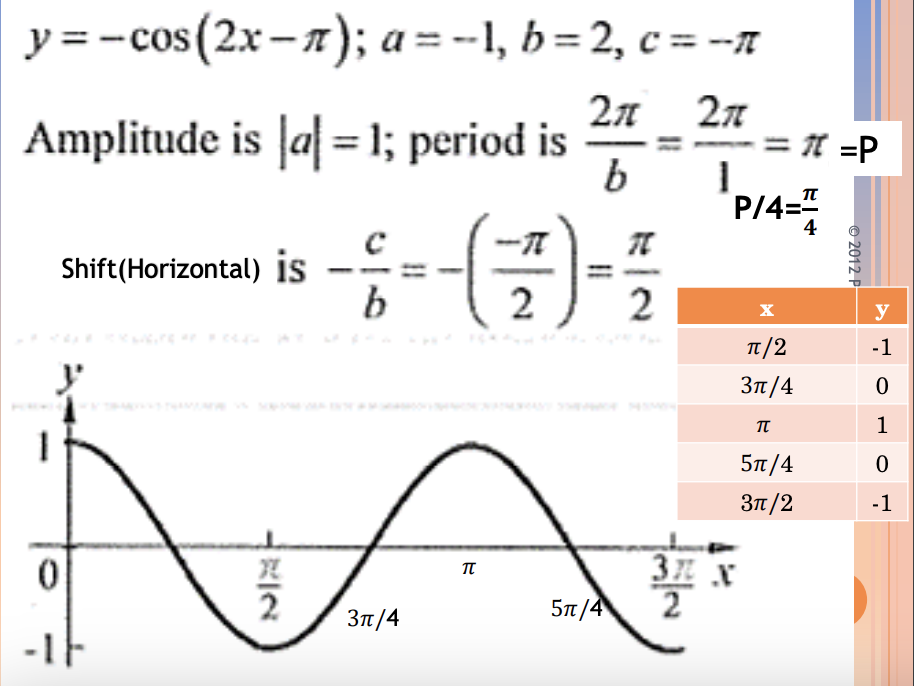
y = -cos(2x - π)
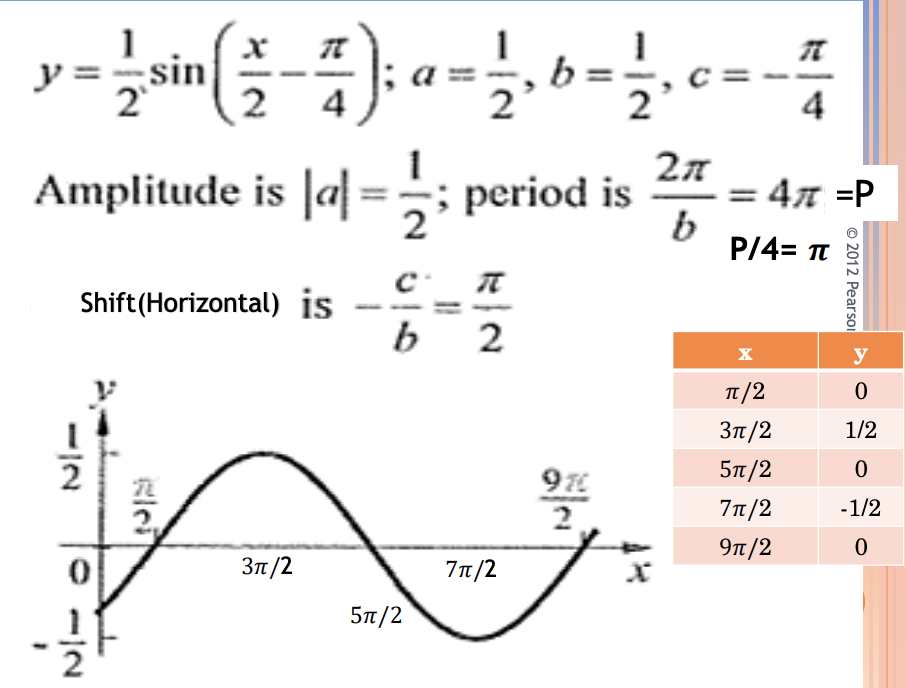
Exercise 3
For the function below:
- a) What is amplitude , ymax and ymin.
- b) What is the period?
- c) What is the shift (horizontal)?
- d) Graph one period and show values at 1/4th of the period, the shift and the amplitude.
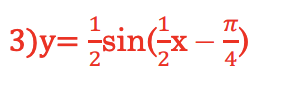
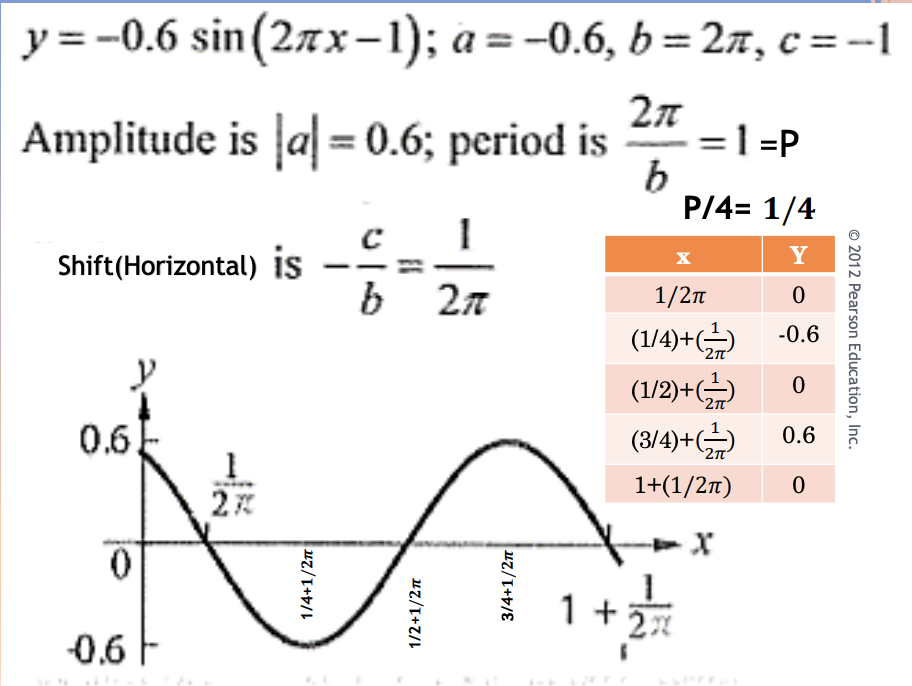
Exercise 4
For the function below:
- a) What is amplitude , ymax and ymin.
- b) What is the period?
- c) What is the shift (horizontal)?
- d) Graph one period and show values at 1/4th of the period, the shift and the amplitude.
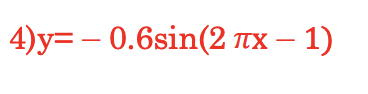
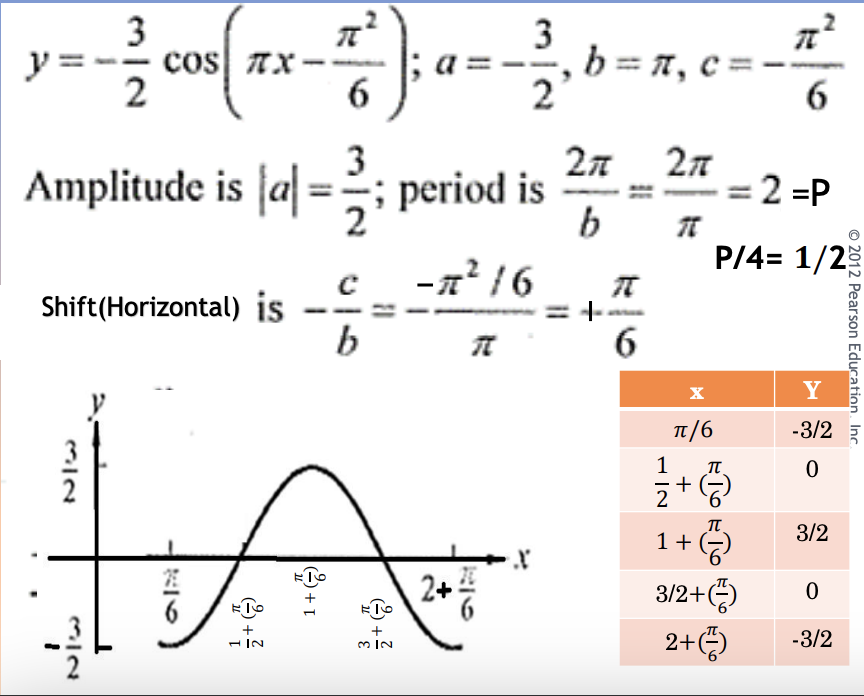
Exercise 5
For the function below:
- a) What is amplitude , ymax and ymin.
- b) What is the period?
- c) What is the shift (horizontal)?
- d) Graph one period and show values at 1/4th of the period, the shift and the amplitude.
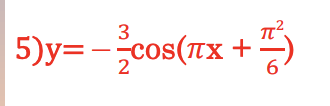

Leave a comment