[Func-Num] 8.6 Exponential and Logarithmic Functions, Applications, and Models

📋 This is my note-taking from what I learned in the class “Math175-002 Functions & Number Systems”

Exponential and Logarithmic Functions, Applications, and Models

1. Exponential Functions and Applications
2. Logarithmic Functions and Applications
3. Exponential-Logarithmic Applications

1. Exponential Functions and Applications

An exponential function with base b, where b > 0 and b != 1, is a function of the form f(x) = b^x, where x is any real number.

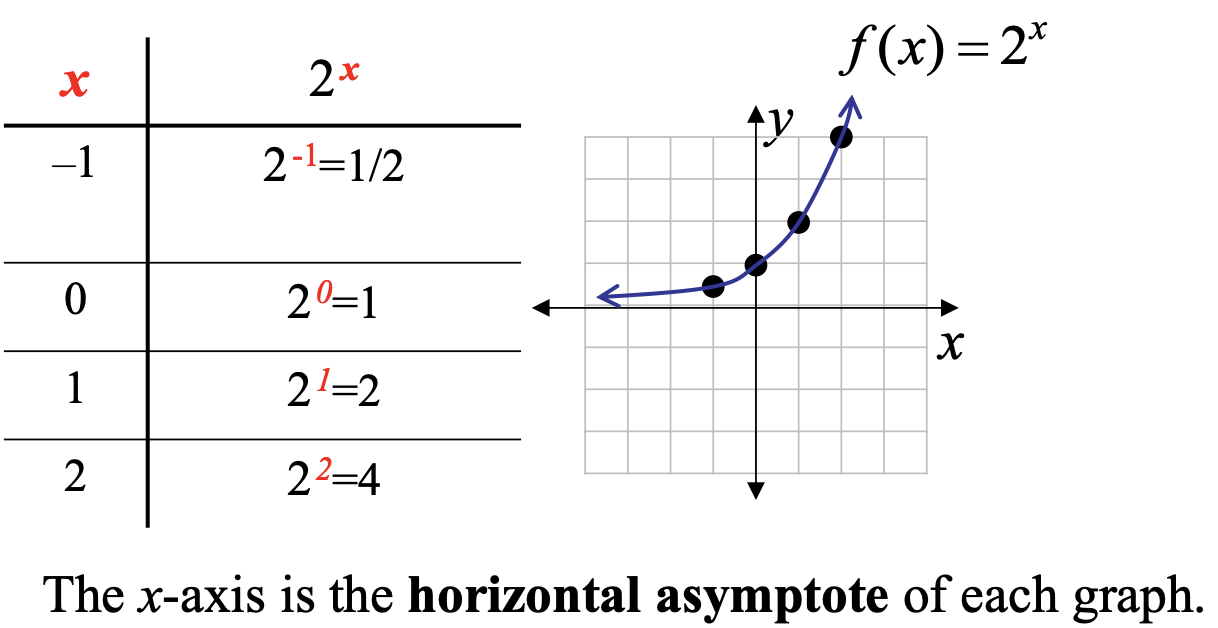
Example: Graph of Exponential Function (b > 1)

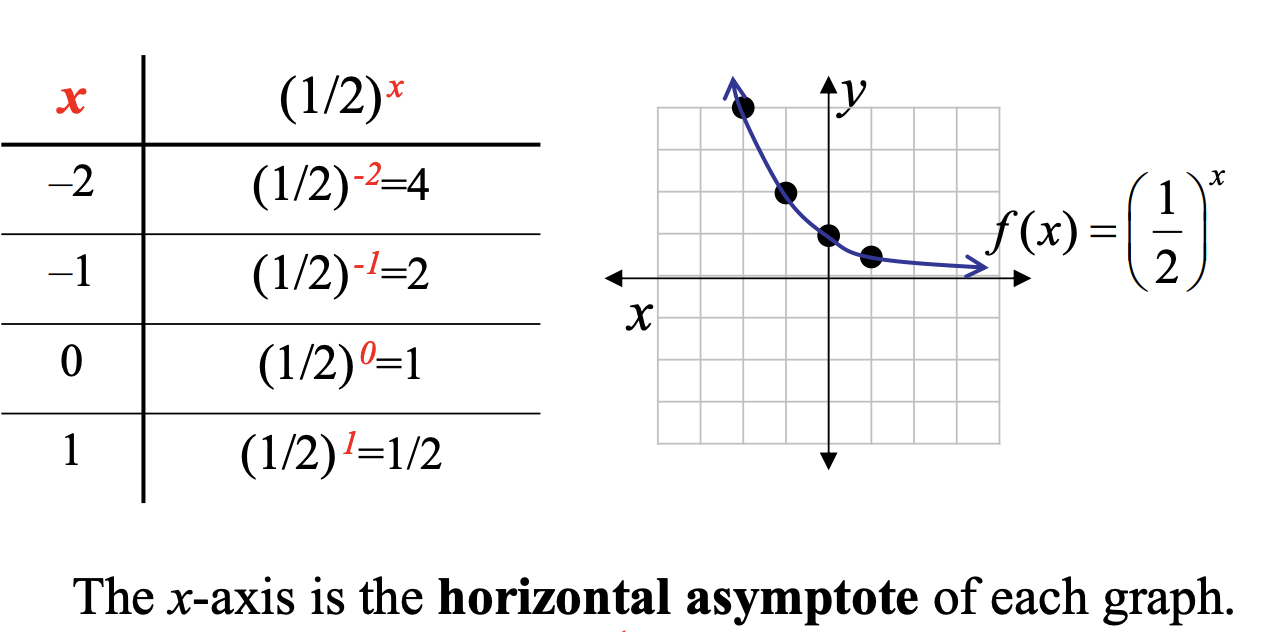
Example: Graph of Exponential Function (0 < b < 1)

1 - A. Graph of f(x) = b^x

1. The graph always will contain the point (0, 1).
2. When b > 1, the graph will rise from left to right. When 0 < b < 1, the graph will fall from left to right.
3. The x-axis is the horizontal asymptote.
4. The domain is (-∞, ∞) and the range is (0, ∞).

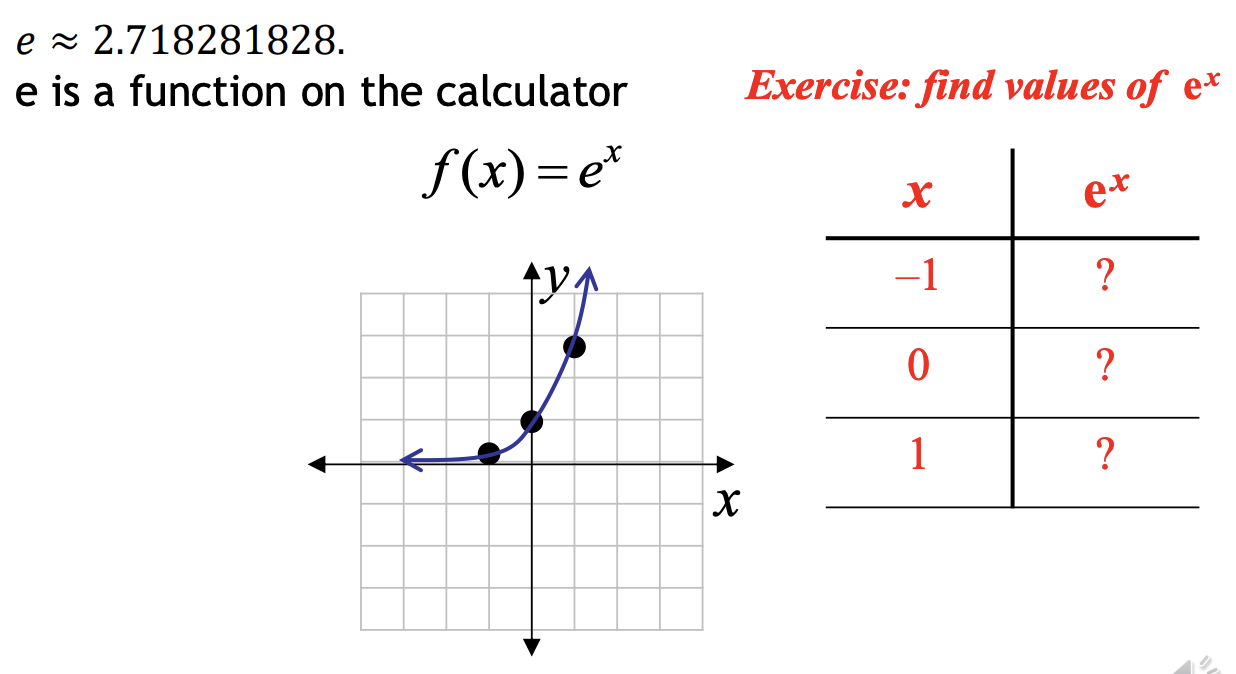
1 - B. Exponential with Base e

1 - C. Compound Interest Formula

Suppose that a principal of P dollars is invested at an annual interest rate r (in percent, expressed as a decimal), compounded n times per year. Then the amount A accumulated after t years is given by the formula

A = P(1 + \({r} \over {n}\) )^nt

Example: Compound Interest Formula

Suppose that $2000 dollars is invested at an annual rate of 8%, compounded quarterly. Find the total amount in the account after 6 years if no withdrawals are made.

Solution
A = P(1 + \({r} \over {n}\))nt
A = 2000(1 + \({0.08} \over {4}\))4(6)
A = 2000(1.02)24 ≈ 2000(1.60844) = 3216.88

There would be $3216.88 in the account at the end of six years.

1 - D. Continuous Compound Interest Formula

Suppose that a principal of P dollars is invested at an annual interest rate r (in percent, expressed as a decimal), compounded continuously. Then the amount A accumulated after t years is given by the formula

A = Pe^rt.

Example: Continuous Compound Interest Formula

Suppose that $2000 dollars is invested at an annual rate of 8%, compounded continuously. Find the total amount in the account after 6 years if no withdrawals are made.

Solution
A = Pert
A = 2000e0.08(6)
A = 2000e0.48 ≈ 2000(1.61607) = 3232.14

There would be $3232.14 in the account at the end of six years.

1 - E. Doubling Time Formula

Time needed to double an initial amount as an exponential function: A = Pe^rt

• A: is present amount
• P: is future amount after t years
• r: is annual compounding rate

Example: Doubling Time

Suppose that a certain amount P is invested at an annual rate of 5% compounded continuously. How long will it take for the amount to double (doubling time)?

Solution
A = Pert	Formula
2P = Pe0.05t	Sub in 2P for A (double)
2 = e0.05t	Divide by P
ln2 = ln e0.05t	Take ln of both sides
ln2 = 0.05t	Simplify
t = \({ln 2} \over {0.05}\) ≈ 13.9	Divide by 0.05

Therefore, it would take about 13.9 years for the initial investment P to double.

2. Logarithmic Functions and Applications

A logarithmic function with base b, where b > 0 and b ≠ 1, is a function of the form

g(x) = log_bx, where x > 0.

2 - A. Graph of g(x) = log_bx

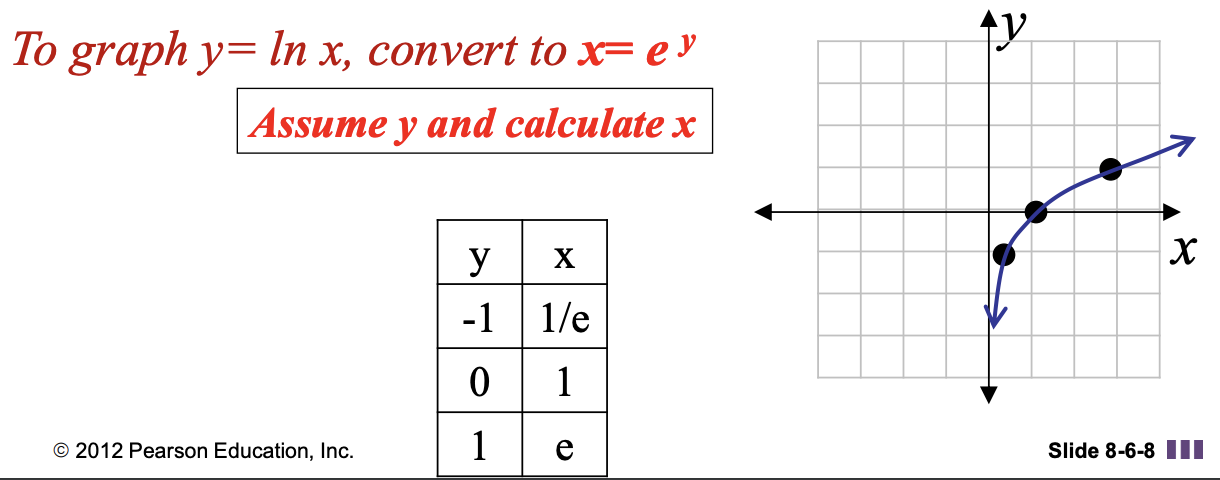
The graph of y = log_bx can be found by interchanging the roles of x and y in the function as shown x = b^y (Exponential Function)

Example: Logarithmic Functions

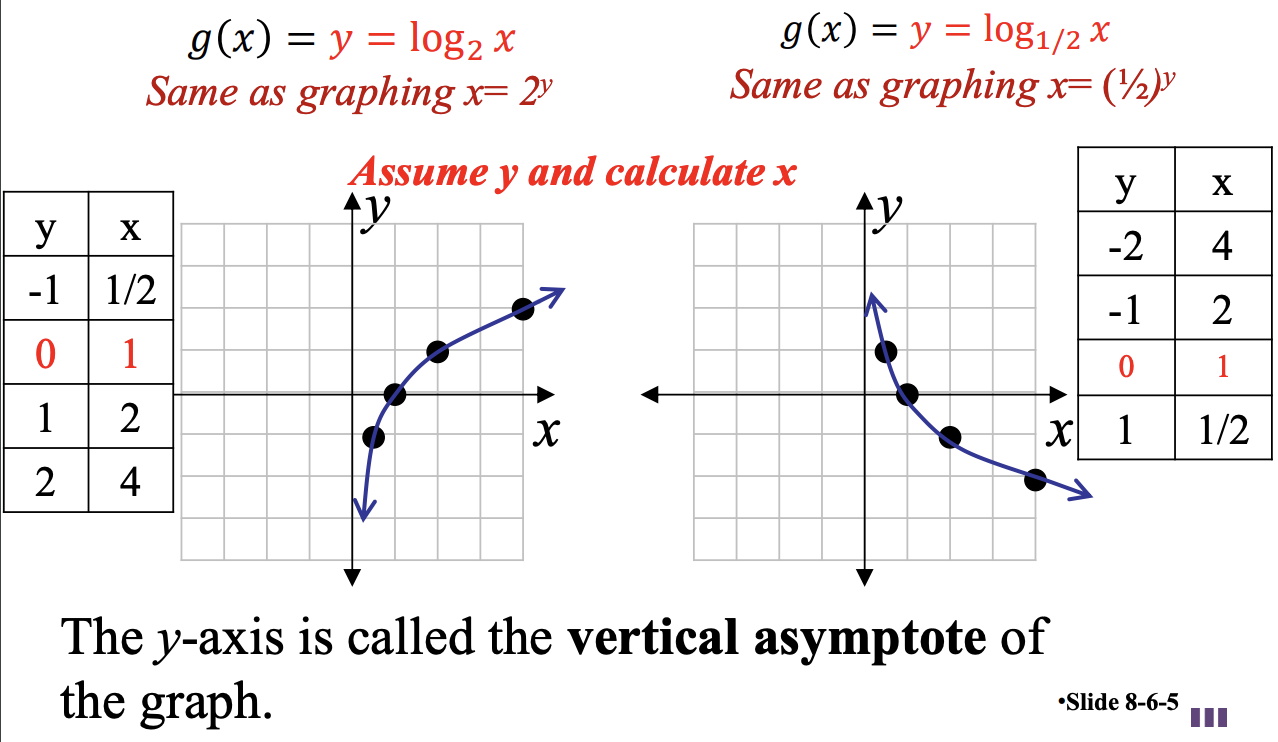
2 - B. Characteristics of Graph g(x) = log_bx

1. The graph always will contain the point (1, 0).
2. When b > 1 the graph will rise from left to right. When 0 < b < 1, the graph will fall from left to right.
3. The y-axis is the vertical asymptote.
4. The domain is (0, ∞) and the range is (-∞, ∞).

2 - C. Natural Logarithmic Function (y = ln x)

“g(x) = y = ln x” is called the natural logarithmic function.

ln x = log_ex, where base e = 2.71828…

The expression ln e^k is the exponent to which the base e must be raised in order to obtain e^k. There is only one such number that will do this, and it is k. Thus for all real numbers k, ln e^k = k. (e = 2.71828…)

2 - D. Models in Nature

Radioactive materials disintegrate according to exponential decay functions. The half-life of a quantity that decays exponentially is the amount of time it takes for any initial amount to decay to half its initial value.

Example : Half-Life

Carbon 14 is a radioactive form of carbon that is found in all living plants and animals. After a plant or animal dies, the radiocarbon disintegrates. The amount of carbon 14 present after t years is modeled by the exponential equation y = y₀e^-0.0001216t

a) What is the half-life of carbon 14?

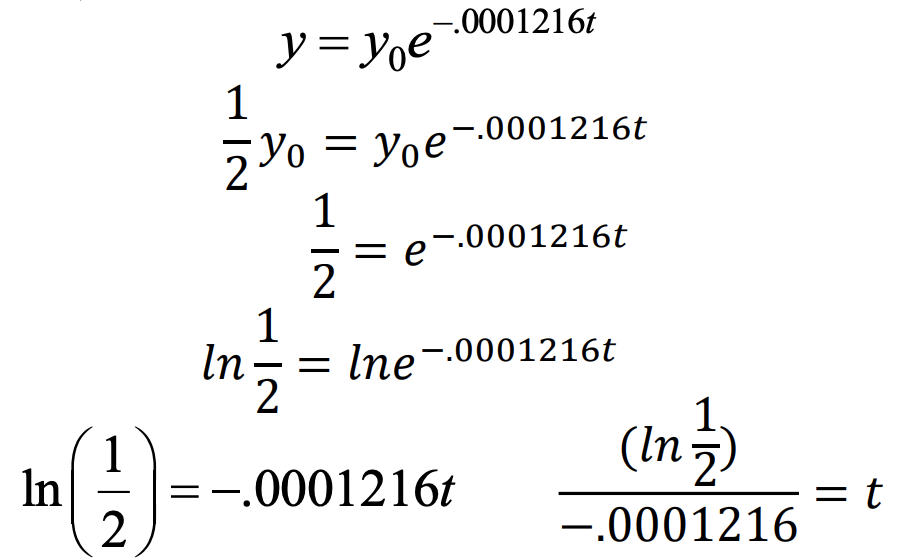
t ≈ 5700 → The half-life of carbon 14 is about 5700 years.

b) If an initial sample contains 1 gram of carbon 14, how much will be left in 10,000 years?

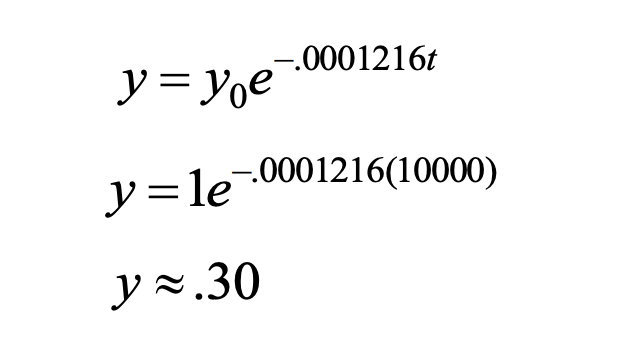
There will be about 0.30 grams remaining.

3. Exponential-Logarithmic Applications (Exponential and Logarithmic Equivalents)

For b > 0 and b ≠ 1, b^y = x, then y = log_bx

Exponential Equation	Logarithmic Equation
34 = 81	4 = log381
104 = 10,000	4 = log1010,000
4-3 = \({1} \over {64}\)	-3 = log4\({1} \over {64}\)
30 = 1	0 = log31

Exercise

Section 8-6: 9~39 (odds), 41, 43, 45, 49, 51

---

Back to Top

See other articles in Category Func-Num