[Func-Num] 7.6 Polynomials and Factoring

Date: 2023.03.02 Updated: 2023.03.02

Categories: Func-Num

📋 This is my note-taking from what I learned in the class “Math175-002 Functions & Number Systems”

Objectives

Identify polynomials using the basic terminology of polynomials.

Add and subtract polynomials.

Multiply polynomials.

Multiply two binomials using the FOIL method.

Find special products of binomials.

Factor the greatest common factor from a polynomial.

Factor a trinomial using the FOIL method in reverse.

Factor a perfect square trinomial and a difference of squares.

Polynomials and Factoring

Basic Terminology
Addition and Subtraction
Multiplication
Special Products
Factoring
Factoring Out the Greatest Common Factor
Factoring by Grouping
Factoring Trinomials
Factoring Special Binomials

1. Basic Terminology

A term, or monomial, is defined to be a number, a variable, or a product of numbers and variables.

Examples: 7, and 8r
A polynomial is a term, or a finite sum or difference of terms, with only nonnegative integer exponents permitted on the variables. If the terms of a polynomial contain only the variable x, then the polynomial is called a polynomial in x. (Polynomials in other variables are defined similarly.)

Example: 3x⁵ + 4x – 1
The expression 9x² - 4x - \({6} \over {x}\) is not a polynomial because of the presence of - \({6} \over {x}\) → The terms of a polynomial cannot have variables in a denominator.
The greatest exponent in a polynomial in one variable is the degree of the polynomial. A non-zero constant is said to have degree 0. (The polynomial 0 has no degree.)

Examples: 3x⁶ - 5x² + 2x + 3 is a polynomial of degree 6 .
A term containing more than one variable has degree equal to the sum of all the exponents appearing on the variables in the term.

Example: 4x²y³z + 3x²y²z has degree 6.

A polynomial containing exactly three terms is called a trinomial and one containing exactly two terms is a binomial.

Polynomial	Degree	Type
9x⁴ - 4x³ + 8x²	4	Trinomial
29x³ + 8x²	3	Binomial
-10x	1	Monomial

2. Addition and Subtraction

Because the variables used in polynomials represent real numbers, a polynomial represents a real number. This means that all the properties of the real numbers hold for polynomials. Here is an application of the distributive property.

Combine like terms: 3x⁵ - 7x⁵ = (3 - 7)x⁵ = -4x⁵
“Like terms” are terms that have the exact same variable factors. Thus, polynomials are added by adding coefficients of like terms and are subtracted by subtracting coefficients of like terms.

Example: Adding and Subtracting Polynomials

Add or subtract as indicated.

a) (4x⁴ - x² - 7x + 9) - (3x⁴ - m² + x - 3) = 4x⁴ - x² - 7x + 9 - 3x⁴ + m² - x + 3 = x⁴ - 8x + 12

As shown in Example, polynomials are often written with their terms arranged in “descending powers.” The term of greatest degree is first, the one with the next greatest degree is second, and so on.

3. Multiplication

The associative and distributive properties, together with the properties of exponents, can also be used to find the product of two polynomials.

Example: Multiplication of Polynomials

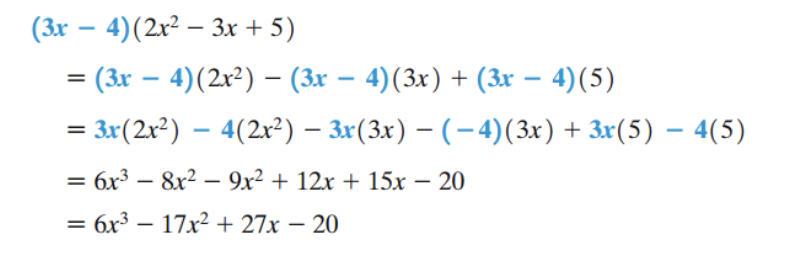
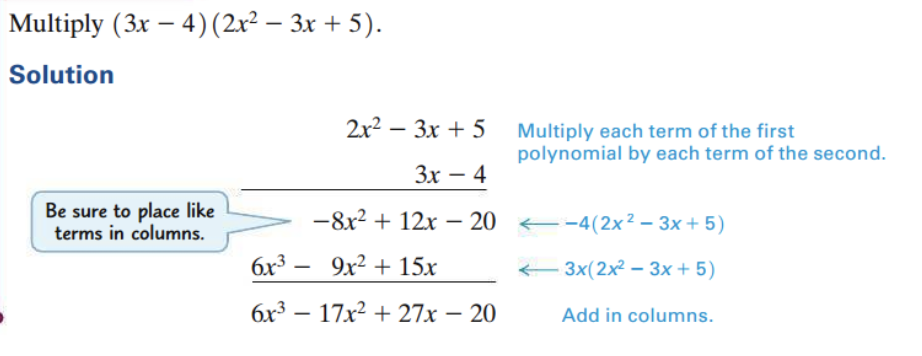
multiplication1 multiplication2

Such a product can be written vertically, as shown in Example 2.

3. Multiplication → FOIL Method

The memory aid “FOIL” is a convenient way to find the product of two binomials. FOIL (for First, Outside, Inside, Last) gives the pairs of terms to be multiplied to get the product.

Example: Multiplication Using the FOIL Method

Foil method

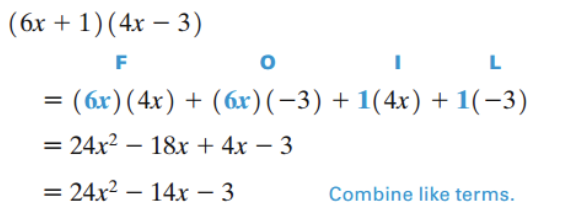
4. Special Products

As shown in Examples 3(b) and (c), the product of two binomials of the forms x + y and x − y is always a binomial. Check that the following is true.

Product of the Sum and Difference of Two Terms

The product x² - y² is called a difference of two squares

(x + y)(x - y) = x² - y²

Squares of Binomials

Squares of binomials are also special products. These are verified by first writing as two factors and then using the FOIL method.

(x + y)² = x² + 2xy + y²

(x - y)² = x² - 2xy + y²

5. Factoring

The process of finding polynomials whose product equals a given polynomial is called factoring. For example, since 4x + 12 = 4(x + 3), both 4 and x + 3 are called factors of 4x + 12. Also, 4(x + 3) is called a factored form of 4x + 12.

A polynomial that cannot be written as a product of two polynomials with integer coefficients is a prime polynomial. A polynomial is factored completely when it is written as a product of prime polynomials with integer coefficients.

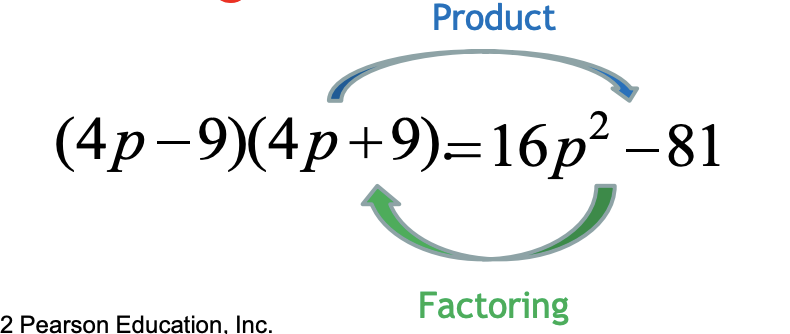
Factoring

Factoring is the inverse of multiplying, so a check requires that the product of the factored form yields the original polynomial.

6. Factoring Out the Greatest Common Factor (GCF)

When factoring a polynomial, we first look for a monomial that is the greatest common factor (GCF) of all the terms of the polynomial.

Some polynomials are factored using the distributive property. We look for a monomial that is the greatest common factor (GCF) of all the terms of the polynomial.

Example: Factoring Out the Greatest Common Factor (GCF)

Factor out the greatest common factor (GCF) from each polynomial.

a) m³(m + 2) − 3m²(m + 2) + m(m + 2) = m(m + 2)(m²(1) - 3m(1) + 1) = m(m + 2)(m² - 3m + 1)

7. Factoring by Grouping

When a polynomial has more than three terms, it can sometimes be factored by a method called factoring by grouping.

Example: Factoring by Grouping

Factor by grouping.

mp² + 4m + 3p² + 12

mp² + 4m	3p² + 12
factor of m	factor of 3

= m(p² + 4) + 3(p² + 4) = (p² + 4)(m + 3)

8.Factoring Trinomials

Factoring trinomials requires using the FOIL method in reverse.

Factoring is the inverse of multiplying.
Since the product of two binomials is usually a trinomial, we can expect factorable trinomials (with no GCF of the terms) to have two binomial factors.
Thus factoring trinomials requires using FOIL in an inverse manner.

Example 1: Factoring Trinomials

Factor 6x² - 7x - 5

To factor this, we must find integers a, b, c, and d such that

6x² - 7x - 5 = (ax + b)(cx + d)
After a few attempts, using FOIL to check, we find

6x² - 7x - 5 = (3x - 5)(2x + 1)

Example 2: Factoring Trinomials

Factor 6x² - 7x - 5

6x² - 7x - 5 = ax² + bx + c
→ a = 6, b = -7, c = -5

Find two numbers such that their:
- Product = ac = 6 * (-5) = -30
- Sum = b = -7
The two numbers are 3 and -10

6x² - 7x - 5 = 6x² + 3x - 10x - 5
Now having 4 terms, factor by grouping:

(6x² + 3x) + (-10x - 5)

= 3x(2x + 1) - 5(2x + 1)

= (3x - 5)(2x + 1)

Perfect Square Trinomials

x² + 2xy + y² = (x + y)²
x² - 2xy + y² = (x - y)²

9. Factoring Special Binomials

Difference of Squares

x² - y² = (x + y)(x - y)

Example: Difference of Squares

Factor each polynomial.

a) 4x² - 9 = (2x)² - 3² = (2x + 3)(2x - 3)

b) 256x⁴ - 625 = (16x²)² - 25² = (16x² + 25)(16x² - 25) = (16x² + 25)(4x + 5)(4x - 5)

Sum and Difference of Cubes

Sum of Cubes:

x³ + y³ = (x + y)(x² - xy + y²)
Difference of Cubes:

x³ - y³ = (x - y)(x² + xy + y²)

Example: Sum and Difference of Cubes

Factor each of the following.

a) 8y³ - 125z⁶ = (2y)³ - (5z²)³
→ x³ - y³ = (x - y)(x² + xy + y²)
= (2y - 5z²)(4y² + 10yz² + 25z⁴)

b) m³ + 27 = m³ + 3³
→ x³ + y³ = (x + y)(x² - xy + y²)
= (m + 3)(m² - 3m + 9)

Seyeon