[Func-Num] 4.4 The Common Computer-Oriented Base Conversions

📋 This is my note-taking from what I learned in the class “Math175-002 Functions & Number Systems”

Base Converter Calculator

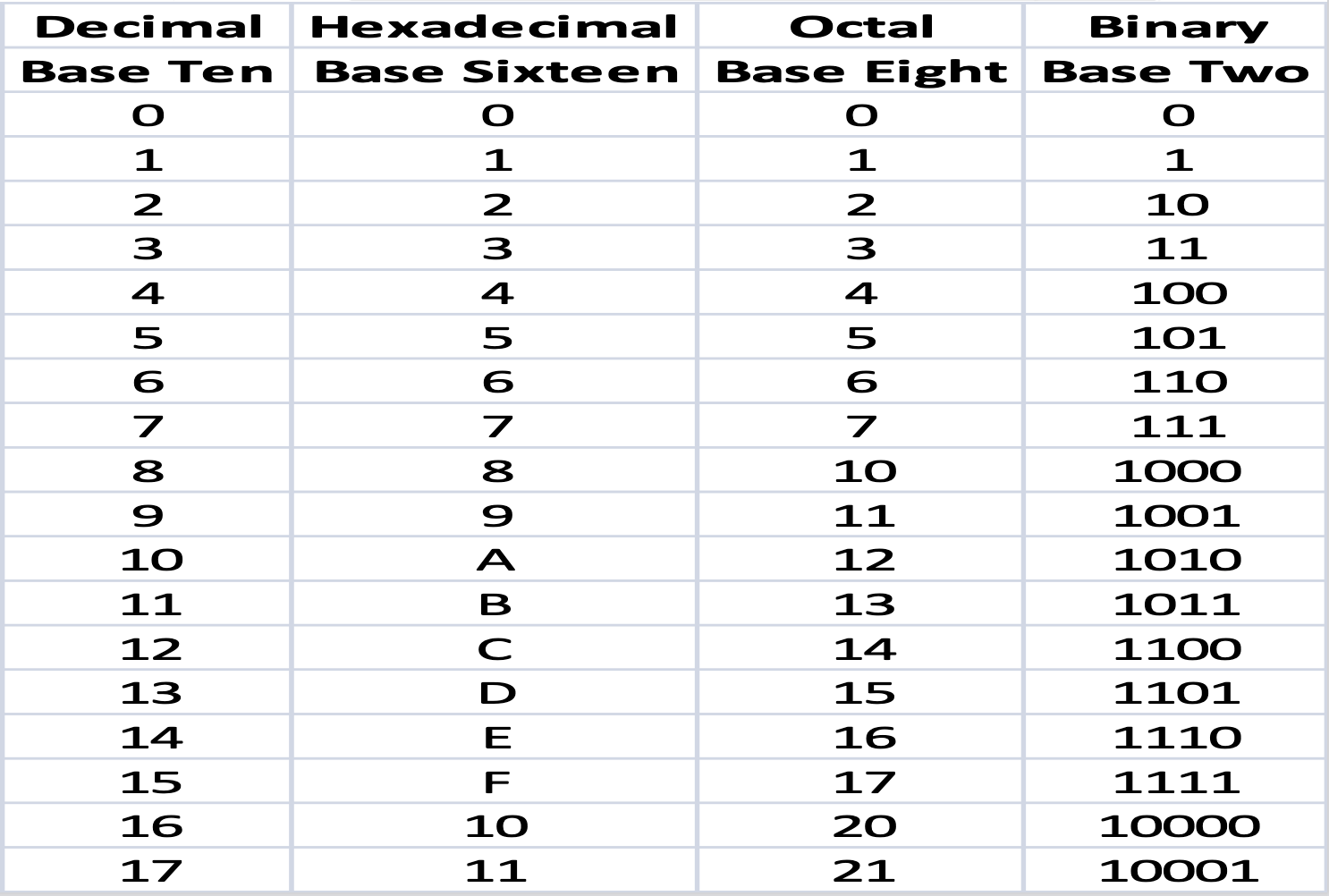
Some Decimal Equivalents in the Common Computer-Oriented Bases

(Use Table to Convert Between Hexadecimal/Binary/Octal)

Example 1: Converting from Octal to Binary

Convert 473_eight to binary form. Each Octal digit is represented by 3 Binary digits

Solution

Octal	4	7	3
Binary	100	111	011

473_eight = 100111011_two

Exercise

Convert 514_eight to binary form.

Solution

Octal	5	1	4
Binary	101	001	100

514_eight = 101001100_two

Example 2: Converting from Binary to Octal

Convert 10011110_two to octal form

Solution

Binary	(0)10	011	110
Octal	2	3	6

(0)10 011 110_two = 236_eight

Exercise

Convert 1101111_{two to Octal form.}

Solution

Binary	(00)1	101	111
Octal	1	5	7

(00)1 101 111_two = 157_eight

Example 3: Converting from Hexadecimal to Binary

Convert 8B4F_sixteen to binary form.

Solution

Each hexadecimal digit yields a 4-digit binary equivalent.

Hexadecimal	8	B	4	F
Binary	1000	1011	0100	1111

8B4F_sixteen = 1000101101001111_two

Exercise

Convert EBD9_sixteen to binary form.

Solution

Hexadecimal	E	B	D	9
Binary	1110	1011	1101	1001

EBD9_sixteen = 1110 1011 1101 1001_two

Example 4: Converting from Binary to Hexadecimal

Convert 10011110_two to hexadecimal form.

Solution

Binary	1001	1110
Hexadecimal	9	E

1001 1110_two = 9E_sixteen

Exercise

Convert (0)1101111_two to Hexadecimal form.

Solution

Binary	(0)110	1111
Hexadecimal	6	F

(0)1101111_two = 6F_sixteen

Exercise

Section 4.4: 5 ~ 47 (odd)

List the first twenty counting numbers in each base.

How to count the Number Bases

• 5: seven (Only digits 0 through 6 are used in base seven.) → 0, 1, 2, 3, 4, 5, 6, 10, 11, 12, 13, 14, 15, 16, 20, 21, 22, 23, 24, 25
• 7: nine (Only digits 0 through 8 are used.) → 0, 1, 2, 3, 4, 5, 6, 7, 8, 10, 11, 12, 13, 14, 15, 16, 17, 18, 20, 21

Write (in the same base) the counting numbers just before and just after the given number. (Do not convert to base ten.)

• 9: 14_five → 13, 20
• 11: B6F_sixteen → B6E, B70 → Solution link: List of Hexadecimal Numbers with base 16 subscripts

Determine, in each base, the least and greatest four-digit numbers and their decimal equivalents.

How to get the least and greatest numbers and decimal 1
How to get the least and greatest numbers and decimal 2

• 13: five → the least: 1000₅ → 125₁₀, the greatest: 4444₅ → 624₁₀

Convert each number to decimal form by expanding in powers and by using the calculator shortcut.

• 15: 3BC_sixteen → 956
• 17: 2356_seven → 874
• 19: 70266_eight → 28854
• 21: 2023_four → 139
• 23: 31544_six → 4312

Convert each number from decimal form to the given base.

• 25: 147 to base sixteen → 93₁₆
• 27: 36401 to base five → 2131101₅
• 29: 587 to base two → 1001001011₂
• 31: 9346 to base six → 111134₆
• 33: 8407 to base three → 102112101₃

Make each conversion as indicated.

• 35: 43_five to base seven → 32₇
• 37: 6748_nine to base four → 1031321₄

Convert each number from octal form to binary form.

• 39: 367_eight → 11110111₂

Convert each number from binary form to octal form.

• 41: 100110111_two → 467₈

Make each conversion as indicated.

• 43: AC_sixteen to binary → 10101100₂
• 45: 101101_two to hexadecimal → 2D₁₆

Identify the greatest number from each list.

• 47: 42_seven, 37_eight, 1D_sixteen → 37_eight

e-Centennial Supplement pages 5 and 6 All. (Answers page: 13)

In problems 1~10, Convert each binary number to a decimal number

• 1: 11 → 3
• 2: 10 → 2
• 3: 100 → 4
• 4: 111 → 7
• 5: 1110 → 14
• 6: 1001 → 9
• 7: 10001 → 17
• 8: 10101 → 21
• 9: 110011 → 51
• 10: 100100 → 36

In problems 11~20, Convert each decimal number to a binary number

• 11: 4 → 100
• 12: 6 → 110
• 13: 11 → 1011
• 14: 27 → 11011
• 15: 57 → 111001
• 16: 63 → 111111
• 17: 99 → 1100011
• 18: 111 → 1101111
• 19: 128 → 10000000
• 20: 200 → 11001000

Change each hexadecimal number to binary format: (Convert each hexadecimal digit to 4-bit binary)

• 1: C4DE → 1100010011011110
• 2: AF → 10101111
• 3: 456B → 100010101101011

Change each binary number to hexadecimal format: (Obtain each hexadecimal digit from the corresponding 4-bit binary segment)

• 4: 100011010111101 → 46BD
• 5: 1110111100001 → 1DE1
• 6: 100101110 → 12E

Write each hexadecimal number in expanded notation, and evaluate its decimal equivalent:

Expanded notation

• 7: 5E0 →

  (5 * 16²) + (14 * 16¹) + (0 * 16⁰)
  = 1280 + 224 + 0 = 1504
  → Decimal equivalent: 1504

• 8: D0C9A →

  (13 * 16⁴) + (0 * 16³) + (12 * 16²) + (9 * 16¹) + (10 * 16⁰)
  = 851968 + 3072 + 144 + 10 = 855194
  → Decimal equivalent: 855194

• 9: 1BEF →

  (1 * 16³) + (11 * 16²) + (14 * 16¹) + (15 * 16⁰)
  = 4096 + 2816 + 224 + 15 = 7151
  → Decimal equivalent: 7151

Use your calculator to convert each decimal number to hexadecimal form:

• 10: 700492 → AB04C
• 11: 32557 → 7F2D
• 12: 51966 → CAFE
• 13: 57007 → DEAF
• 14: 3243 → CAB
• 15: 47806 → BABE

Convert the following decimal numbers to binary form: (Hint: You will find that the numbers are too large for a 10-digit calculator to convert to binary mode, but you can use your calculator to change from decimal to hexadecimal, and then convert the answers from hexadecimal to binary as in questions 1-3)

• 16: 56789 → 1101110111010101
• 17: 987 → 1111011011
• 18: 3030 → 101111010110

Convert the binary numbers to decimal form: (Hint: Change them by hand to hexadecimal from, as in questions 4-6 and then use your calculator to convert from hexadecimal to decimal)

• 19: 110100011011100 → 26844
• 20: 101111011111101 → 24317

---

Back to Top

See other articles in Category Func-Num