[Func-Num] 6.5 General Base Conversions

📋 This is my note-taking from what I learned in the class “Math175-002 Functions & Number Systems”

General Base Conversions

• We consider bases other than ten. Bases other than ten will have a spelled-out subscript as in the numeral 54_eight
• When a number appears without a subscript assume it is base ten; 96
• Note that 54_eight is read “five four base eight.” → Do Not read it as “fifty-four.”

Powers of Alternative Bases

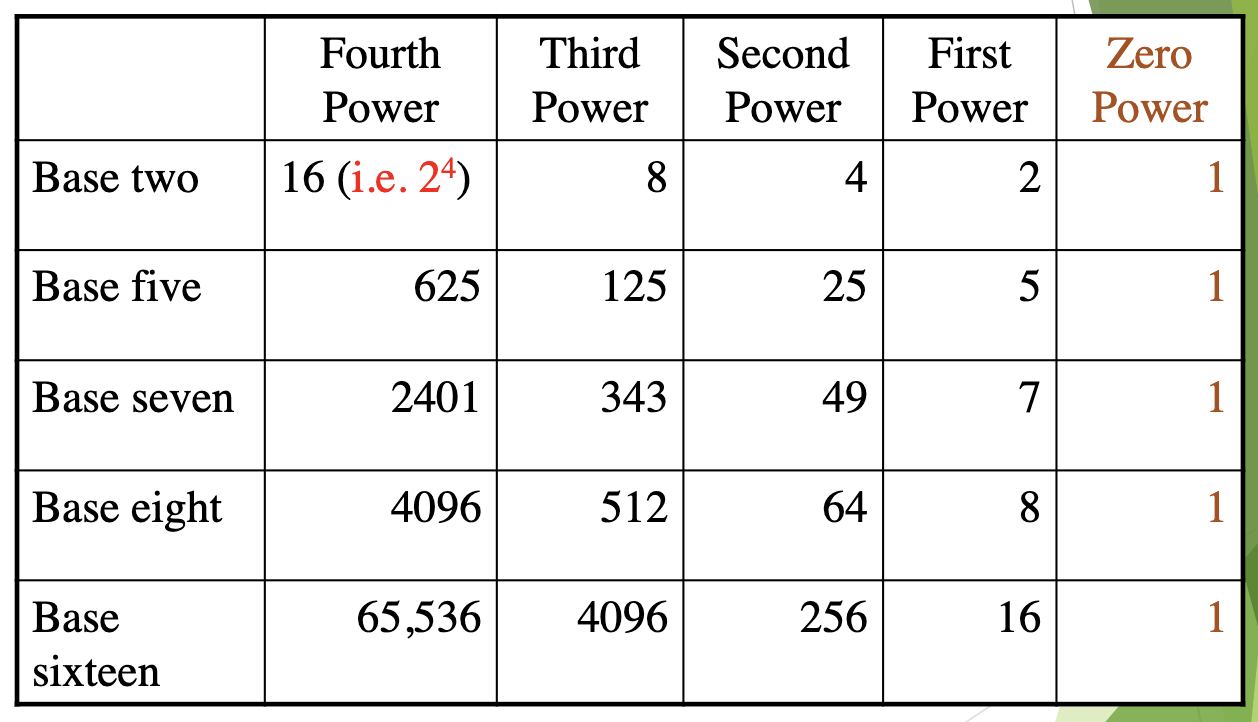
Example 1: Converting Bases to Decimal

Convert 2134_five to decimal form using expanded form. → Number has four digits -> Maximum power of base is 4 - 1 = 3

Solution

2134_five
= 2( \(5^{3}\) ) + 1( \(5^{2}\) ) + 3( \(5^{1}\) ) + 4( \(5^{0}\) ) → Exponent starts with “3”(Cuz maximum power of base is “3”)
= (2*125) + (1*25) + (3*5) + 4
= 250 + 25 + 15 + 4
= 294

Exercise

Convert 234_five to decimal form using expanded form. (Hint: Maximum power of base five is 3-1=2)

Solution

234_five
= 2( \(5^{2}\) ) + 3( \(5^{1}\) ) + 4( \(5^{0}\) ) → Exponent starts with “2”(Cuz maximum power of base is “2”)
= (2*25) + (3*5) + 4
= 50 + 15 + 4
= 69

Calculator Shortcut for Base Conversion to Decimal

To convert from another base to decimal form:

• Start with the first digit on the left and multiply by the base.
• Then add the next digit, multiply again by the base, and so on.
• The last step is to add the last digit on the right. Do not multiply it by the base.

Example 2: Calculator Shortcut for Base Conversion to Decimal

Use the calculator shortcut to convert 432134_five

to decimal form.

Solution

432134_five
= ((((4*5 + 3)*5 + 2)*5 + 1)*5 + 3)*5 + 4
= 14669

Exercise

Use the calculator shortcut to convert 321_four to decimal form.

Solution

321_four
= (3*4 + 2)*4 + 1
= 57

Example 3: Converting from Decimal to Another Base

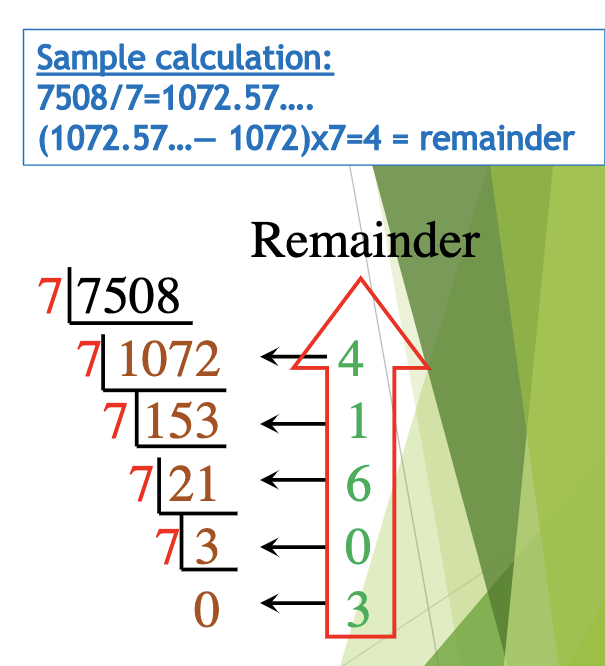
Convert 7508 to base seven.

Solution

• Divide by 7, record the resulting whole number and remainder as shown.
• Then divide the resulting whole number by 7, and record the resulting whole number and remainder again.
• Repeat until resulting whole number is zero.
• From the remainders (bottom to top) we get the answer: 7508 = 30614_seven

Exercise

Convert 8619 to base eight.

Solution

8619 = 20653_eight

Converting Between Two Bases Other Than Ten

Many people feel the most comfortable handling conversions between arbitrary bases (where neither is ten) by going from the given base to base ten and then to the desired base.

Example: Convert from Base 7 to Base 5

Base 7
→ Extended OR Calculator →
Base 10(Decimal)
→ Long division AND Remainder →
Base 5

Example 4: Converting Between Two Bases Other Than Ten

Convert 3164_seven to base 5.

Solution

3164_seven

= (((3*7 + 1)*7 + 6)*7 + 4) = 1124(Decimal)

1124(Decimal) = 13444₅

Exercise

Convert 4275_nine to base six.

Solution

4275_nine = (((4*9 + 2)*9 + 7)*9 + 5 = 3146

3146 = 22322₆

Computer Mathematics

• There are three alternative base systems that are most useful in computer applications.
• These are binary (base two), octal (base eight), and hexadecimal (base sixteen) systems.
• Computers and handheld calculators use the binary system.

Example 5: Converting from Binary to Decimal

Convert 111001_two to decimal form.

Solution

111001_two

= ((((1*2 + 1)*2 + 1)*2 + 0)*2 + 0)*2 + 1 = 57

Exercise

Convert 1100111_two to decimal form.

Solution

1100111_two = (((((1*2 + 1)*2 + 0)*2 + 0)*2 + 1)*2 + 1)*2 + 1 = 103

Example 6: Converting from Decimal to Binary

Convert 39 to binary.

Solution

39 = 100111_two

Exercise

Convert 19 to binary.

Solution

19 = 10011_two

Example 7: Converting from Decimal to Octal

Convert 9583 to octal form.

Solution

Divide repeatedly by 8, writing the remainders at the side. From the remainders (From bottom to top), 9583 = 22557_eight

Exercise

Convert 8472 to Octal form.

Solution

8472 = 20430_eight

Example 8: Converting from Octal to Decimal

Convert 654301_eight to decimal form.

Solution

654301_eight
= ((((6*8 + 5)*8 + 4)*8 + 3)*8 + 0)*8 + 1
= 219329

Exercise

Convert 156_eight to decimal form.

Solution

156_eight = 110

Example 9: Converting from Hexadecimal to Decimal

Computer programmers commonly use the letter A, B, C, D, E, and F as hexadecimal digits for the numbers ten through fifteen, respectively.

• A: 10
• B: 11
• C: 12
• D: 13
• E: 14
• F: 15

Convert FA5_sixteen to decimal form.

Solution

FA5_sixteen
= (15 * \({16}^{2}\) ) + (10 * \({16}^{1}\) ) + (5 * \({16}^{0}\) )
= 3840 + 160 + 5
= 4005

Exercise

Convert ED9_sixteen to Decimal.

Solution

ED9_sixteen
= 3801

Example 10: Converting from Decimal to Hexadecimal

Convert 748 from decimal form to hexadecimal form.

Solution

Use repeated division by 16. From the remainders at the right, 748 = 2EC_sixteen

Exercise

Convert 859 decimal to hexadecimal form.

Solution

859 = 35B_sixteen

---

Back to Top

See other articles in Category Func-Num