[Func-Num] 6.3 Rational Numbers and Decimal Representation
Categories: Func-Num
📋 This is my note-taking from what I learned in the class “Math175-002 Functions & Number Systems”
Objectives
- Define and identify rational numbers
- Write a rational number in lowest terms
- Add, subtract, multiply, and divide rational numbers in fraction form
- Solve a carpentry problem using operations with fractions
- Apply the density property and find arithmetic mean
- Convert a rational number in fraction form to a decimal number
- Convert a terminating or repeating decimal to a rational number in fraction form
Definiton and the Fundatmental Property
Rational Numbers
Rational numbers = { \({x \over x}\) is a quotient of two integers, with denominator not 0}
Fundamental Property of Rational Numbers
If a, b, and k are integers with b≠0 and k≠0, then the following holds true
\({(a*k) \over (b*k)}\) = \({a \over b}\)
Q. Write \({36 \over 54}\) in lowest terms
A. \({36 \over 54}\) = \({(18*2) \over (18*3)}\) = \({2 \over 3}\)
- A rational number is in lowest terms if the greatest common factor of the numerator (top number) and the denominator (bottom number) is 1
- Rational numbers are written in lowest terms using the following property
Cross-Product Test for Equality of Rational Numbers
For rational numbers \({a \over b}\) and \({c \over d}\) , where b≠0, d≠0, the following holds true
\({a \over b}\) = \({c \over d}\) if and only if ad = bc
- If the product of the “extremes”(a and d) equals the product of the “means”(b and c), the fractions are equal → This is the cross-product test
Operations with Rational Numbers
Adding and Subtracting Rational Numbers
If \({a \over b}\) and \({c \over d}\) are rational numbers, then the following hold true
\({a \over b}\) + \({c \over d}\) = \({(ad+bc) \over (bd)}\) and \({a \over b}\) - \({c \over d}\) = \({(ad-bc) \over (bd)}\)
- This formal definition is seldom used in practice
- We usually first rewrite the fractions with the least common multiple of their denominators, called the least common denominator (LCD)
- LCD Calculator - Least Common Denominator
Conversions Involving Mixed Numbers
Fractions that are greater than 1 may be expressed in mixed number form
The mixed number form of \({3 \over 2}\) is 1 \({1 \over 2}\)
E.g. 2 \({5 \over 8}\) to a fraction → \({16 \over 8}\) + \({5 \over 8}\) = \({21 \over 8}\)
E.g. \({86 \over 5}\) to a mixed number → 17 \({1 \over 5}\)
(The quotient is the whole number part of the mixed number, The remainder is the numerator of the fraction part, while the divisor is the denominator)
- The whole number part and the fraction part of a mixed number are added (even though no addition symbol is shown)
Multiplying Rational Numbers
If \({a \over b}\) and \({c \over d}\) are rational numbers, then the following holds true
\({a \over b}\) * \({c \over d}\) = \({ac \over bd}\)
- A multiplication problem such as this is often solved by using slash marks(/) to indicate that common factors have been divided out of the numerator and denominator
Definition of Division
If a and b are real numbers, where b≠0, then the following holds true
\({a \over b}\) = a * \({1 \over b}\)
- A fraction bar indicates the operation of division - The multiplicative inverse of the nonzero number b is \({1 \over b}\) → We define division using the multiplicative inverse
- To divide fractions, invert the divisor and multiply
Dividing Rational Numbers
If \({a \over b}\) and \({c \over d}\) are rational numbers, where \({c \over d}\) ≠ 0, then the following holds true
\({a \over b}\) / \({c \over d}\) = \({a \over b}\) * \({d \over c}\) = \({ad \over bc}\)
Density and the Arithmetic Mean
There is no integer between two consecutive integers, such as 3 and 4. However, a rational number can always be found between any two distinct rational numbers. For this reason, the set of rational numbers is said to be dense.
Density Property of the Rational Numbers
If r and t are distinct rational numbers, with r<t, then there exists a rational number s such that
r < s < t
- There are infinitely many rational numbers between two distinct rational numbers
- One example of a rational number that is between two distinct rational numbers is the arithmetic mean of the two numbers
- To find the arithmetic mean, or average, of n numbers, we add the numbers and then divide the sum by n
- For two numbers, the number that lies halfway between them on a number line is their average.
Decimal Form of Rational Numbers
- Rational numbers can be expressed as decimals
- Decimal numerals have place val-ues that are powers of 10
Terminating decimal
- A decimal such as 0.375, which stops, is called a terminating decimal
Repeating decimal
- A decimal such as 0.36…, which continues indefinitely, is called a repeating decimal → To indicate this, we write a bar (called a vinculum over the “block” of digits that repeats
- While we distinguish between terminating and repeating decimals in this text, some mathematicians prefer to consider all rational numbers as repeating decimals. This can be justified by thinking this way: If the division process leads to a remain-der of 0, then zeros repeat without end in the decimal form.
- By considering the possible remainders that may be obtained when converting a quotient of integers to a decimal, we can draw an important conclusion about the decimal form of rational numbers. If the remainder is never zero, the division will produce a repeating decimal. This happens because each step of the division process must produce a remainder that is less than the divisor. Since the number of different possible remainders is less than the divisor, the remainders must even-tually begin to repeat. This makes the digits of the quotient repeat, producing a repeating decimal.
Decimal Representation of Rational Number
Any rational number can be expressed as either a terminating decimal or a repeating decimal
Criteria for Terminating and Repeating Decimals
- A rational number \({a \over b}\) in lowest terms results in a terminating decimal if the only prime factor of the denominator is 2 or 5 (or both)
- A rational number \({a \over b}\) in lowest terms results in a repeating decimal if a prime other than 2 or 5 appears in the prime factorization of the denominator.
- Must a terminating decimal or a repeating decimal represent a rational number? → The answer is yes.
How to write a repeating decimal as a quotient of integers
Q.
A.

Exercise
Section 6.3: 11 ~ 17 (odd)
Choose the expression(s) that is(are) equivalent to the given rational number
- 11: 4/8 → A.1/2, C.0.5
- 13: 5/9 → C.0.5(Repeating 5)
Write each fraction in lowest terms
- 15: 16/48 → 1/3
- 17: -15/35 → -3/7
Section 6.3: 29 ~ 45 (odd)
Perform the indicated operations and express answers in lowest terms. Use the order of operations as necessary.
- 29: 3/8 + 1/8 = 4/8 = 1/2
- 31: 5/16 + 7/12 = 15/48 + 28/48 = 43/48
- 33: 2/3 - 7/8 = 16/24 - 21/24 = -5/24
- 35: 5/8 - 3/14 = 35/56 - 12/56 = 23/56
- 37: 3/4 * 9/5 = 27/20 = 1 7/20
- 39: -2/3 * -5/8 = 5/12
- 41: 5/12 / 15/4 = 1/9
- 43: -9/16 / -3/8 = 3/2 = 1 1/2
- 45: (1/3 / 1/2) + 5/6 = 3/2 = 1 1/2
Section 6.3: 57 ~ 61 (odd)
- 57: 9/16 + 2(5/8) - 1/2 = 21/16
- 59: 9(2 1/2) + 3(5 1/8) = 37 7/8
- 61: 5(1/16) + 3(2 1/2) - 7/16 = 7 6/16
Section 6.3: 79 ~ 83 (odd)
Find the rational number halfway between the two given rational numbers.
- 79: 1/2, 3/4 → (1/2 + 3/4) / 2 = 5/8
- 81: 3/5, 2/3 → (3/5 + 2/3) / 2 = 19/30
- 83: -2/3, -5/6 → {(-2/3) + (-5/6)} / 2 = -3/4

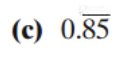

Leave a comment