[Disc-Math] C.12 Logic Gates

📋 This is my note-taking from what I learned in the class “Math185-002 Discrete Mathematics”

Overview of Course

Topics

• Logic Gates

Weekly Learning Outcomes

• Simplify expression using Boolean algebra.
• Represent Boolean expressions with logic diagrams.

1. Logic Gates

Logic Gates

Boolean expressions correspond to logic gates

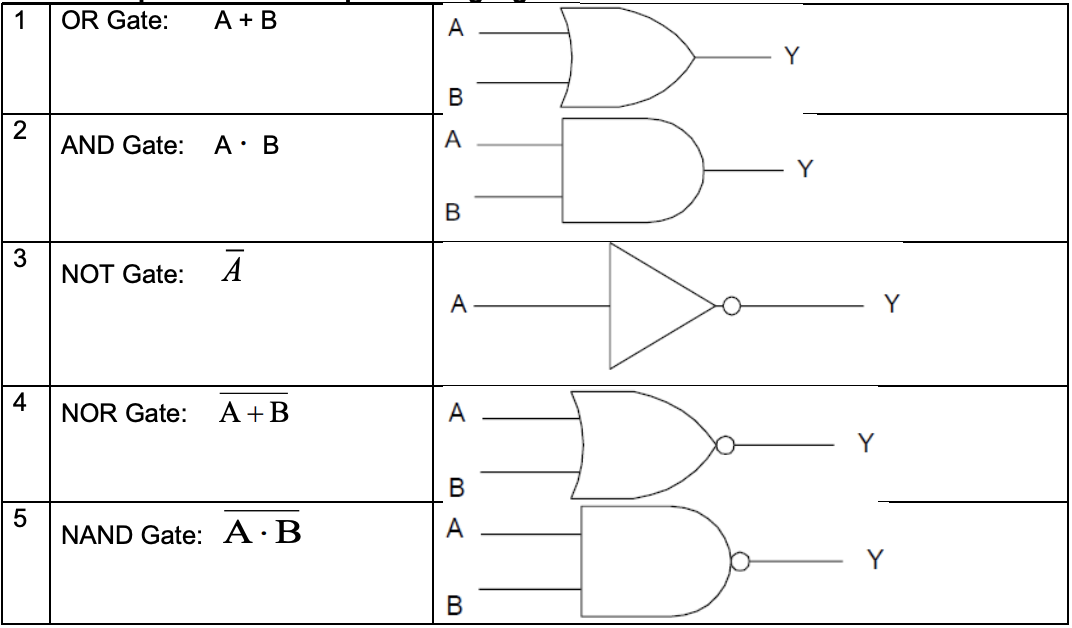
Logic Gate Truth Tables

		OR	AND	NOT	NOR	NAND
A	B	A+B	A*B	\(\overline{A}\)	\(\overline{A+B}\)	\(\overline{A*B}\)
0	0	0	0	1	1	1
0	1	1	0	1	0	1
1	0	1	0	0	0	1
1	1	1	1	0	0	0

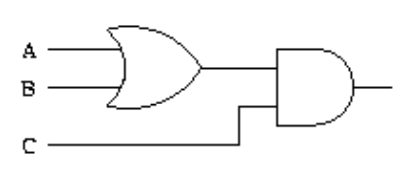
Example 1:

Draw a logic circuit for (A+B)C.

Solution:

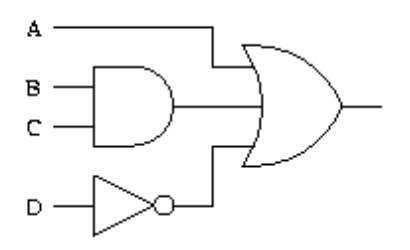
Example 2:

Draw a logic circuit for A + BC + \(\overline{D}\).

Solution:

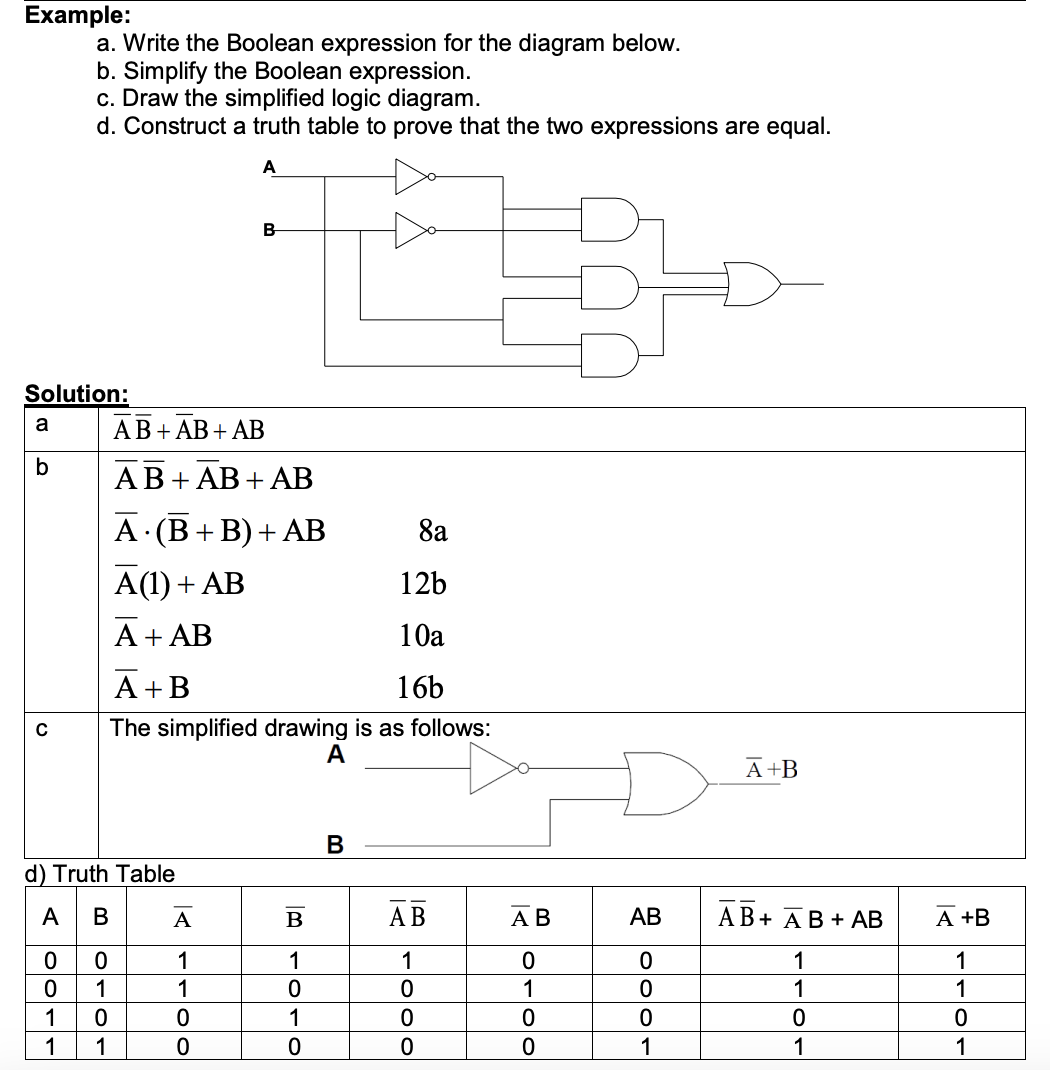
Example 3:

Write the Boolean expression for the diagram below.

Solution:

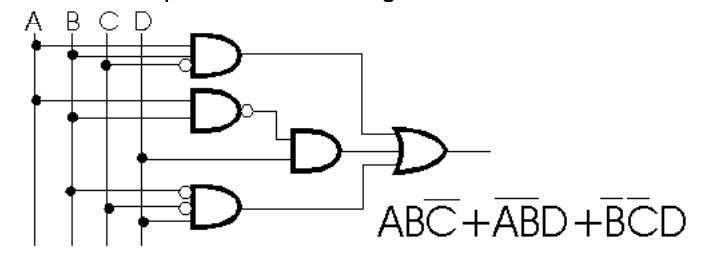
Example 4:

Write the Boolean expression for the diagram below.

Solution:

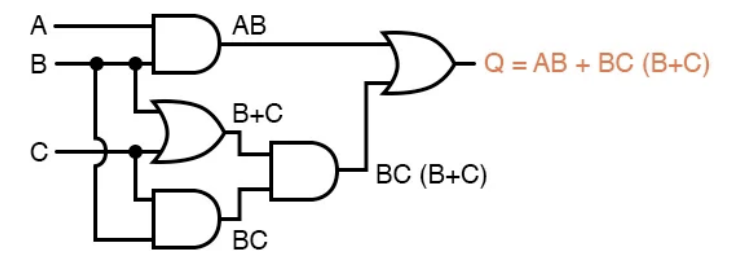
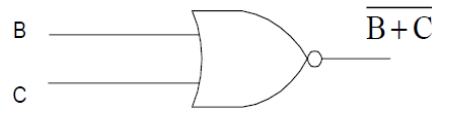
Example 5:

• a) Write the Boolean expression for the diagram below.
• b) Simplify the Boolean expression.
• c) Draw the simplified logic diagram.

Solution:

• a) \(\overline{AB}\) * \(\overline{B + C}\)

• b)

  

• c) The simplified drawing is as follows:

  

Example 6:

Practice Logic Gates

Logic Gate	Boolean Algebra
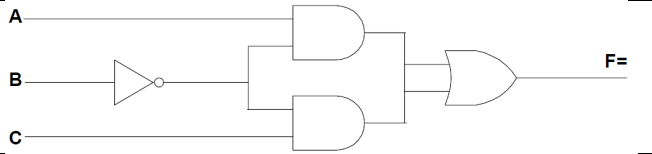	F = A \(\overline{B}\) + \(\overline{B}\) C; F = \(\overline{B}\) (A + C)
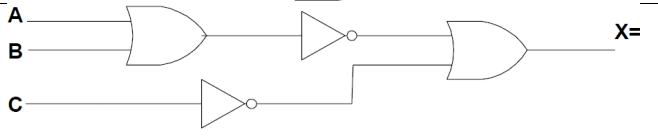	X = \(\overline{A + B}\) + \(\overline{C}\)
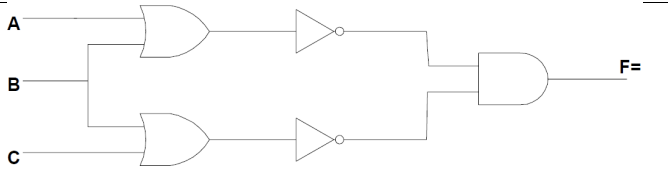	F = (\(\overline{A + B}\))(\(\overline{B + C}\)); F = \(\overline{A + B + C}\)
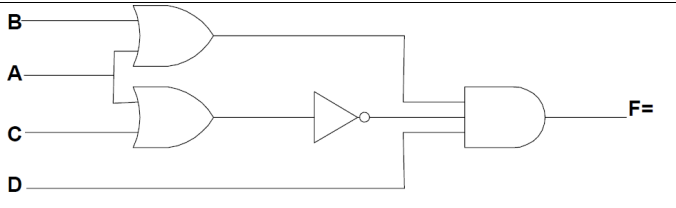	F = (A + B)(\(\overline{A + C}\))D; F = \(\overline{A}\) B \(\overline{C}\) D
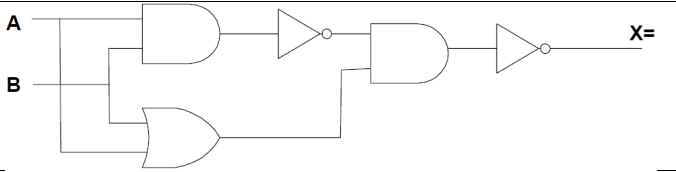	X = \(\overline{ \overline{AB} (A + B)}\); X = \(\overline{A + B}\) + AB
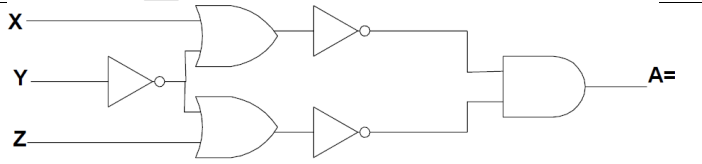	A = \(\overline{(X + \overline{Y})}\) \(\overline{(\overline{Y} + Z)}\); A = \(\overline{X}\) Y \(\overline{Z}\)

2. Implementation of Truth Tables

Implementation of a truth table is the process of translating a table of data (the truth table – which describes inputs and outputs) into a circuit diagram.

Sum-Of-Products, or SOP, Boolean expressions may be generated from truth tables quite easily, by determining which rows of the table have an output of 1, writing one product term for each row, and finally summing all the product terms. This creates a Boolean expression representing the truth table as a whole. Sum-Of-Products expressions lend themselves well to implementation as a set of AND gates (products) feeding into a single OR gate (sum).

Procedure:

1. For any row which has an output (Y) value of 1 write the Boolean product for the variables’ truth values in that particular row.
2. Write a Boolean expression for the output as a sum of the products found in step 1.
3. Simplify the resulting Boolean expression (if possible) to draw a circuit diagram.

Remarks:

• The Boolean expression obtained from the truth table is not necessarily the most efficient. It may be possible to simplify this expression which would indicate a more efficient circuit design.

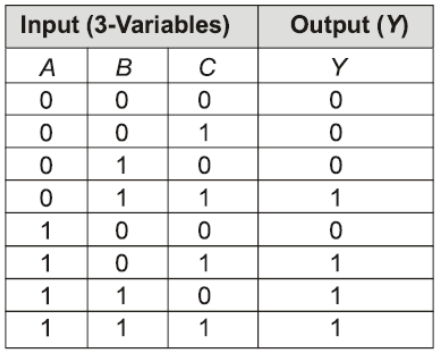
Example: Write a Boolean expression

SOP & POS

Practice SOP & POS

Truth Table	Write a Boolean expression	Simplify the Boolean expression
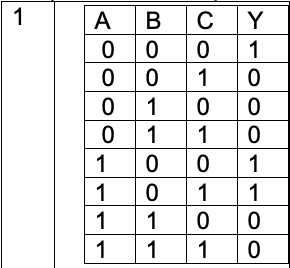	Y = \(\overline{A}\) \(\overline{B}\) \(\overline{C}\) + A \(\overline{B}\) \(\overline{C}\) + A \(\overline{B}\) C	Y = \(\overline{B}\) (\(\overline{C}\) + A)
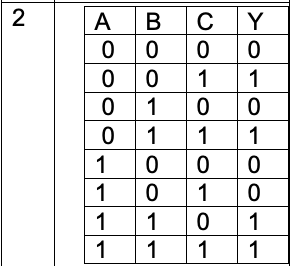	Y = \(\overline{A}\) \(\overline{B}\) C + \(\overline{A}\) BC + AB \(\overline{C}\) + ABC	\(\overline{A}\) C + AB
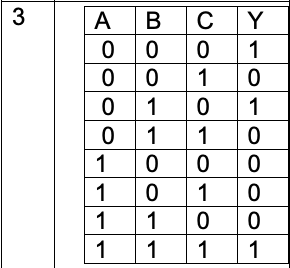	Y = \(\overline{A}\) \(\overline{B}\) \(\overline{C}\) + \(\overline{A}\) B \(\overline{C}\) + ABC	Y = \(\overline{A}\) \(\overline{C}\) + ABC
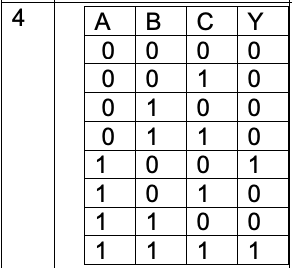	Y = A \(\overline{B}\) \(\overline{C}\) + ABC	Y = A(\(\overline{B + C}\) + BC)
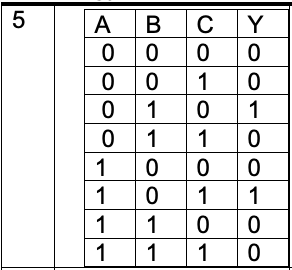	Y = \(\overline{A}\) B \(\overline{C}\) + A \(\overline{B}\) C	Y = \(\overline{A}\) B \(\overline{C}\) + A \(\overline{B}\) C
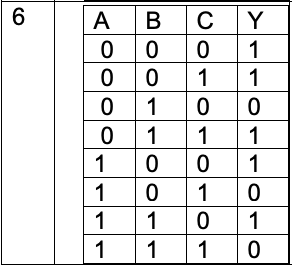	Y = \(\overline{A}\) \(\overline{B}\) \(\overline{C}\) + \(\overline{A}\) \(\overline{B}\) C + \(\overline{A}\) BC + A \(\overline{B}\) \(\overline{C}\) + AB \(\overline{C}\)	Y = \(\overline{A}\) (\(\overline{B}\) + C) + A \(\overline{C}\)

---

Back to Top

See other articles in Category Disc-Math