[Disc-Math] C.11 Truth Tables and Boolean Algebra
Categories: Disc-Math
Tags: Boolean Truth Tables
📋 This is my note-taking from what I learned in the class “Math185-002 Discrete Mathematics”
Overview of Course
Topics
- Analyzing Arguments with Truth Tables
- Boolean Algebra
Weekly Learning Outcomes
- Analyze arguments with truth tables and by comparing to the valid/invalid forms.
- Simplify expression using Boolean algebra.
3.6 Analyzing Arguments with Truth Tables
Analyzing Arguments with Truth Tables
Testing the Validity of an Argument with a Truth Table
- Step 1: Assign a letter to represent each component statement in the argument.
- Step 2: Express each premise and the conclusion symbolically.
- Step 3: Form the symbolic statement of the entire argument by writing the conjunction of all the premises as the antecedent of a conditional statement, and the conclusion of the argument as the consequent.
- Step 4: Complete the truth table for the conditional statement formed in Step 3. If it is a
tautology, then the argument isvalid; otherwise it is invalid.
[(p → q) ∧ p] → q
Example: Determine whether the argument is valid or invalid.
- If there is a problem, then I must fix it.
- There is a problem.
- I must fix it.
Solution:
- p: There is a problem
- q: I must fix it
| First premise is | Second Premise is | Conclusion |
|---|---|---|
| p → q | p | q |
=> [(p → q) ∧ p] → q
To decide if this argument is valid, we must determine whether the conjunction of both premises implies the conclusion for all possible combinations of truth values for p and q. Therefore, write the conjunction of the premises as the antecedent of a conditional statement, and write the conclusion as the consequent.

To Test for Validity Construct a Truth Table For [(p → q) ∧ p] → q
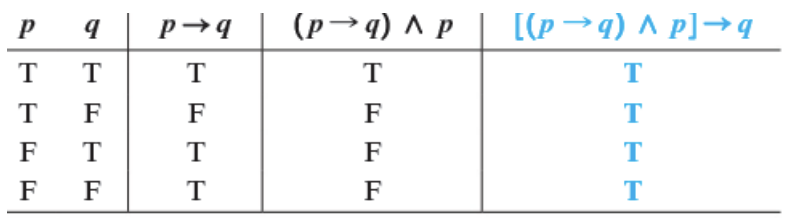
Because the final column, shown in color, indicates that the conditional statement that represents the argument is true for all possible truth values of p and q, the statement is a tautology. Thus, the argument is valid.
[(p → q) ∧ q] → p
Example: Determine whether the argument is valid or invalid.
- If we arrive at the bus stop before the bus arrives, we will grab cotton candy.
- We order cotton candy.
- We arrive at the bus stop before the bus arrives.
Solution:
- p: We arrive at the bus stop before the bus arrives
- q: We order cotton candy
| First premise is | Second Premise is | Conclusion |
|---|---|---|
| p → q | q | p |
=> [(p → q) ∧ q] → p
To Test for Validity Construct a Truth Table For [(p → q) ∧ q] → p

The last column of the truth table contains an F, so the argument is invalid.
[(p → q) ∧ ~q] → ~p
Example: Determine if the argument is valid or invalid.
- If I can avoid sweets, I can avoid the dentist.
- I can’t avoid the dentist.
- I can’t avoid sweets.
Solution:
Let p represent “I can avoid sweets” and q represent “I can avoid the dentist.”
p → q
\[{~q} \over {~p}\]| [(p → q) | ∧ | ~q] | → | ~p |
|---|---|---|---|---|
| Premise | And | Premise | Implies | Conclusion |
The truth table for this argument indicates a tautology, and the argument is valid.

The pattern of reasoning of this example is called “Modus Tollens,” or the law of contraposition, or indirect reasoning.
Valid Argument Forms
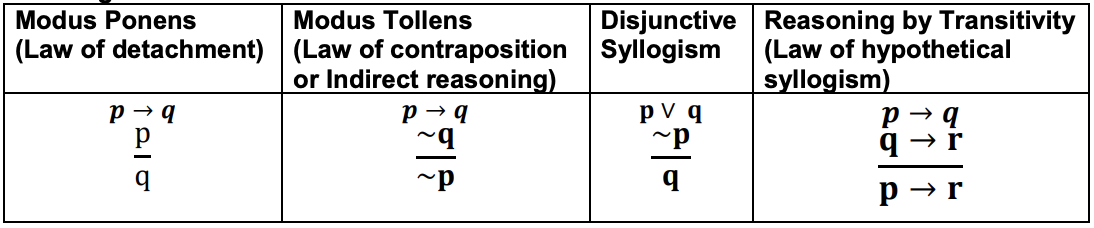
Invalid Argument Forms (Fallacies)

Example 1: Determine whether the argument is valid or invalid.
- If Eddie goes to town, then Mabel stays at home.
- If Mabel does not stay at home, then Rita will cook.
- Rita will not cook.
- Therefore, Eddie does not go to town.
Solution:
Let p represent “Eddie goes to town,” let q represent “Mabel stays at home,” and let r represent “Rita will cook.”
[(p → q) ∧ (~q ∧ r) ∧ ~r] → ~p
Because the final column does not contain all Ts, the statement is not a tautology and the argument is invalid.
Example 2: Decide whether the argument is valid or a fallacy and give the form that applies.
“A mathematician is a device for turning coffee into theorems.”
\[{You turn coffee into Theorems} \over {You are a mathematician}\]Solution:
- p: You are a mathematician
- q: You turn coffee into theorem
p → q
\[{q} \over {p}\]Since this is the form “fallacy of the converse,” it is invalid and considered fallacy.
Example 3: Decide whether the argument is valid or a fallacy and give the form that applies.
“If you’re going through hell, keep going.” (quote from Winston Churchill)
\[{You are not going through hell} \over {Don't Keep going}\]Solution:
- p: You are going through hell.
- q: Keep going.
p → q
\[{~p} \over {~q}\]Since this is the form “fallacy of the inverse,” it is invalid and considered fallacy.
Example 4: Decide whether the argument is valid or a fallacy and give the form that applies.
“If you use binoculars, then you get a glimpse of the bald eagle.”
\[{If you get a glimpse of a bald eagle, then you'll be amazed} \over {If you use binoculars, then you'll be amazed}\]Solution:
- p: You use binoculars
- q: You get a glimpse of a bald eagle
- r: You will be amazed
p → q
\[{q → r} \over {p → r}\]Since this is the form “reasoning by transitivity,” it is a valid and considered true.
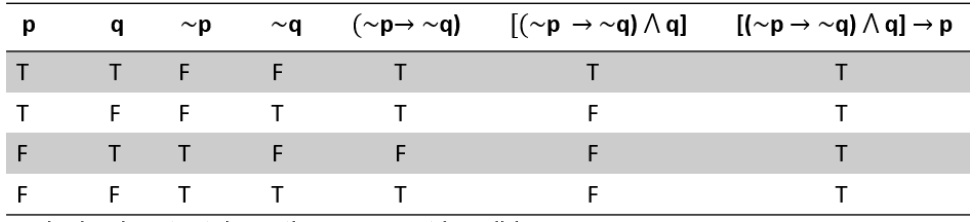
Example 5: Use the truth table to determine whether the argument is valid or invalid.
~p → ~q
\[{q} \over {p}\]Solution:
Conditional Statement: [(~p → ~q) ∧ q] → p
The conclusion is a tautology, the argument is valid.
Boolean Algebra
Boolean algebra is a division of mathematics that deals with operations on logical values and incorporates binary variables. Boolean algebra is specifically used for two-valued logic (True/False, 1/0, open/closed etc.). A Boolean algebra is an algebraic structure that incorporates the properties of set operations (union, intersection, and complement) and logic operations (OR, AND, and NOT).
Definitions: There are three operations defined as followed
-
- Disjunction or a logical sum (OR function)
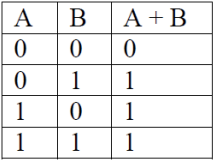
-
- Conjunction or a logical product (AND function)
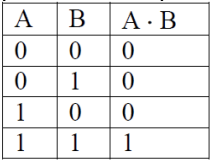
-
- Negation (NOT function)
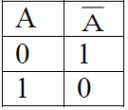
The first two operators are binary since it combines or operates on two elements of a set to produce another element of the set. The last operation is unary since it combines or operates on a single element of a set to produce another element of the set.
Note: the only result in these three definitions, which contradicts ordinary arithmetic, is 1 + 1 = 1.
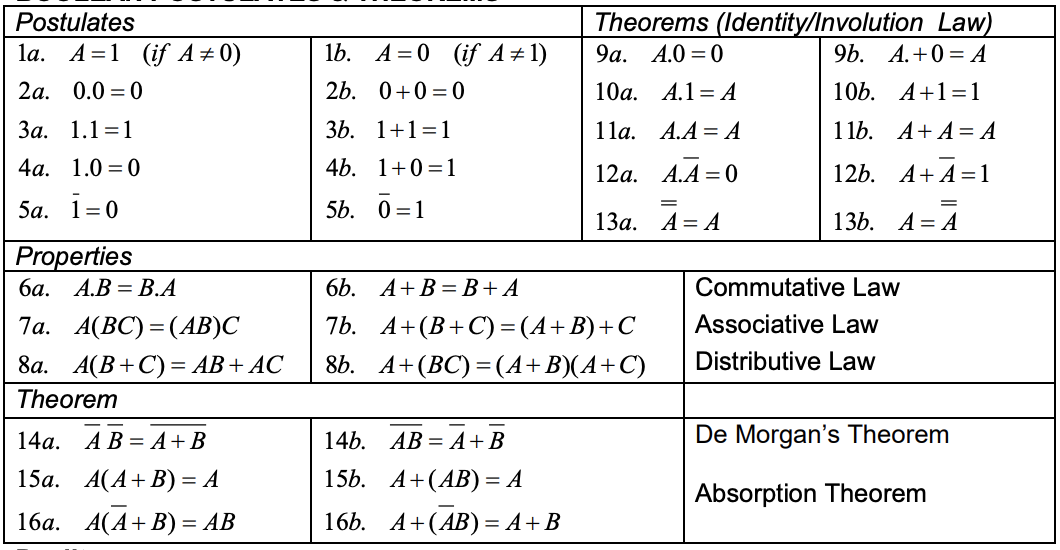
Boolean Postulates & Theorems
Duality
A true Boolean algebra expression can be converted into another true Boolean algebra expression by making the following substitutions.
1 ⟷ 0 and · ⟷ +
Example 1: Simplifying Boolean Expressions
- (AB)(BC)
- A + B + AC + AB
Solution:
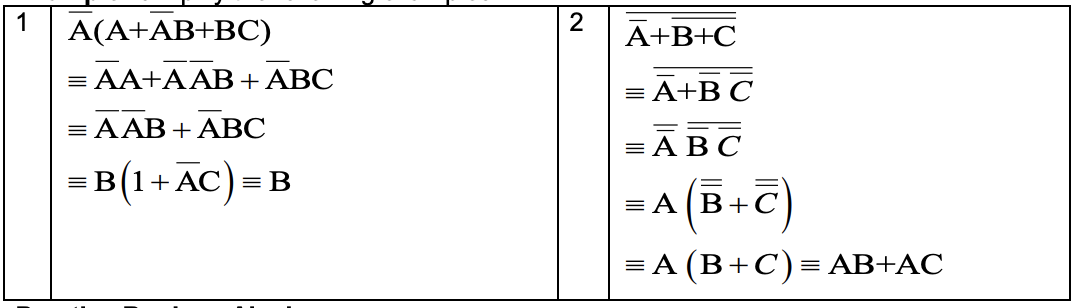
Example 2: Simplify the following examples


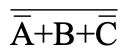

Leave a comment