[Disc-Math] C.10 The Conditional and Circuits

Date: 2023.07.27 Updated: 2023.07.27

Categories: Disc-Math

Tags: Circuits Conditional

📋 This is my note-taking from what I learned in the class “Math185-002 Discrete Mathematics”

Overview of Course

Topics

The Conditional and Circuits
More on The Conditional

Weekly Learning Outcomes

Evaluate the truth value of conditional statements.
Identify the converse, inverse, and contrapositive of a conditional statement.
Evaluate the truth value of a bi-conditional statement.

3.3 The Conditional and Circuits

The Conditional and Circuits

Conditionals

A conditional statement is a compound statement that uses the connective if…then.
The conditional is written with an arrow, so “if p then q” is symbolized p -> q we read this as “p implies q” or “if p then q.” The statement p is the antecedent, while q is the consequent.

Example 1:

You will fail when you do not study. It has similar meaning as: If you do not study, (then) you will fail.

Example 2:

If you run the red, (then) you will get a ticket. (Note: that the conditional connective does not imply a cause-and-effect relationship.)

You run the red - You get a ticket

You run the red - You don’t get a ticket

You don’t run a red - You get a ticket

You don’t run a red - You don’t get a ticket

Note: The conditional connective (if…then) may sometimes be hidden.

Truth Table for the Conditional “p → q”

p	q	p → q
T	T	T
T	F	F
F	T	T
F	F	T

Note: The statement “if p then q” is true in all cases, except when p is true and q is false.

Special Characteristics of Conditional Statements

p → q is false only when the antecedent is true and the consequent is false.
If the antecedent is false, then p → q is automatically true.
If the consequent is true, then p → q is automatically true.

Example 1: Finding the Truth Value of a Conditional

Given that p, q, and r are all false, find the truth value of the following statement.

(p → ~q) → (~r → q)

Solution:

Using the shortcut method, we can replace p, q, and r with F

(p → ~q) → (~r → q)

(F → ~F) → (~F → F)

(F → T) → (T → F)

T → F

F

The statement (p → ~q) → (~r → q) is false when p, q, and r are all false.

Example 2: Determining Whether Conditionals Are True or False

Write true or false for each statement. Here T represents a true statement, and F represents a false statement.

a) T → 17 = 32

b) (8 < 2) → F

c) (4 ≠ 3 + 1) → T

Solution:

a) Because the antecedent is true, while the consequent, 7 = 3, is false, the given statement is false by the first point mentioned above.

b) The antecedent is false, so the given statement is true by the second observation.

c) The consequent is true, making the statement true by the third characteristic of conditional statements.

Example 3:

Decide whether each statement is True or False (T represents a true statement, F represents a false statement).

a) (3 > 8) → T => Answer : False

b) (7 = 5) → F => Answer : True

Example 4: Constructing Truth Table

(~p → ~q) → (~p ⋀ q)

Solution:

Tautology

A statement that is always true, no matter what the truth values of the components, is called a tautology. (We may check by forming truth tables)

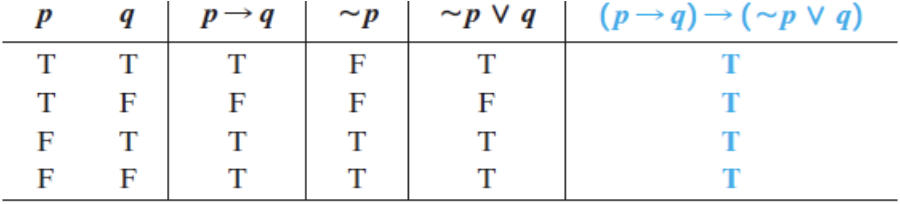
Example 1: Constructing Truth Table

(p → q) → (~p ⋁ q)

Solution:

Several other examples of tautologies:

p ⋁ ~p, p → p, and (~p ⋁ ~q) → ~(p ⋀ q)

Different Forms of Conditional

Writing a Conditional as an “or” (disjunction) Statement

p → q is equivalent to ~p ⋁ q.
Negation of a Conditional

The negation of Negation of p → q is equivalent to ~p ⋁ q.

Applying De Morgan’s law: ~(p → q) ≡ ~(~p ⋁ q) ≡ p ⋀ ~q

Example 1:

Determine the negation of each statement.

If you call her, she will ignore. → Answer: You call her, and she will not ignore.

All dogs love bones. → Answer: All dogs’ love bones has similar meaning as “if it is a dog, it loves bones.” It is a dog and it does not love bones.

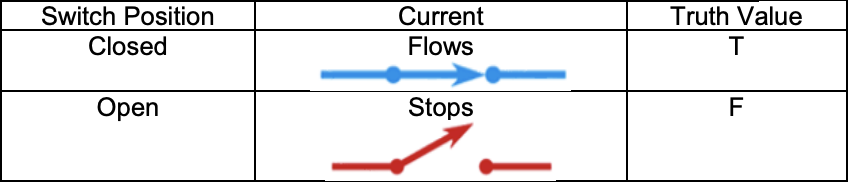
Circuits

Current will flow through switch when it is closed and not when it is open.

Series Circuit

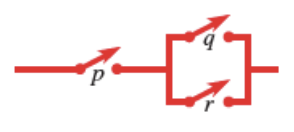
Figure below shows two switches connected in series. In series connection, current will flow only when both switches are closed.

Series circuit resembles the conjunction (and) p ⋀ q.

p ⋀ q is true only when both p and q are true.

Parallel Circuit

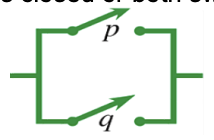
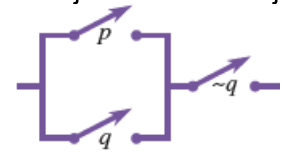
Figure below shows two switches connected in parallel. In parallel connection, current will flow only when either of the switch is closed or both switches are closed.

Parallel circuit resembles the disjunction (or) p ⋁ q.

p ⋁ q is true only when either p or q are true, or both are true.

The circuit in the above figure corresponds to the statement “(p ⋁ q) ⋀ ~q, which is a compound statement involving both a conjunction and a disjunction.

Some Equivalent Statements to Simplify Circuits

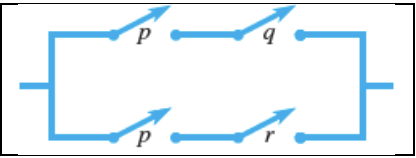
Example 1:

Simplify the circuit shown below.

Solution:

p and q are connected in series with each other which is equivalent to p ⋀ q

p and r are connected in series with each other which is equivalent to p ⋀ r

These two series connected in parallel with each other which is equivalent to (p ⋀ q) ⋁ (p ⋀ r)

(p ⋀ q) ⋁ (p ⋀ r) ≡ p ⋀ (q ⋁ r)

Logical Equivalence

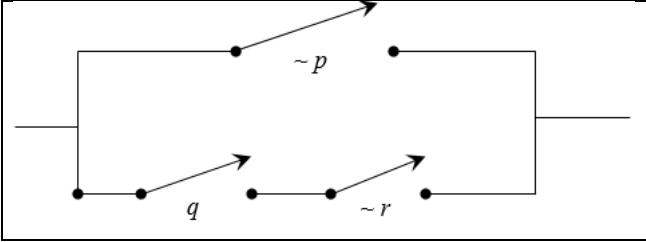
Example 1:

Draw a circuit for p → (q ⋀ ~r)

Solution:

Writing a Conditional as an “or” (disjunction) Statement (I added). The equivalent simplified expression is p → (q ⋀ ~r) ≡ ~p ⋁ (q ⋀ ~r)

3.4 More on The Conditional

Converse, Inverse, and Contrapositive

In a conditional statement p → q, p is called antecedent, and q is called consequent.

If antecedent p and consequent q are interchanged, A new conditional statement q → p is formed which is called converse of the given conditional statement.
If antecedent p and consequent q are both negated, A new conditional statement ~p → ~q is formed which is called inverse of the given conditional statement.
If antecedent p and consequent q both are interchanged and negated, A new conditional statement ~q → ~p is formed which is called contrapositive of the given conditional statement.

Summary

Conditional Statement	p → q	If p, then q
Converse	q → p	If q, then p
Inverse	~p → ~q	If not p, then not q
Contrapositive	~q → ~p	If not q, then not p

Truth Table for Conditional, Converse, Inverse, and Contrapositive Statements

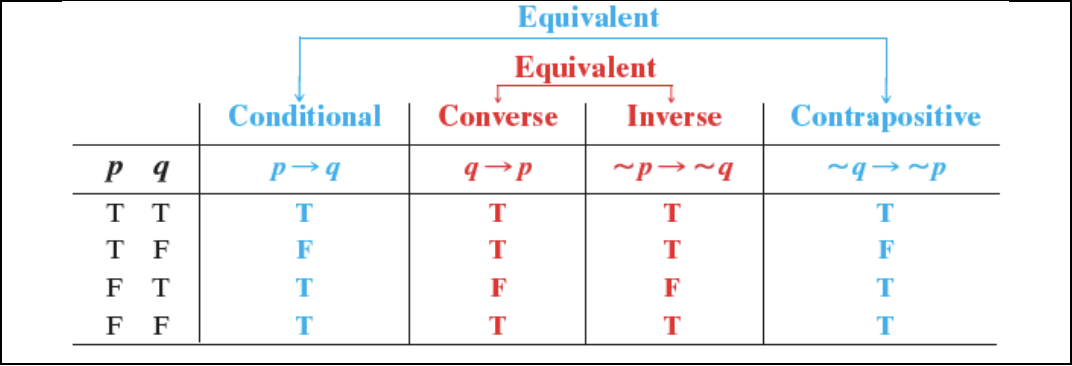
Note: A conditional statement and its contrapositive are equivalent, and the converse and inverse are equivalent.

Example 1:

Given the conditional statement, If I am a student, then I attend school,

Determine: a) The converse b) The inverse c) The contrapositive.

Solution:

a) Converse: If I attend school, then I am a student.

b) Inverse: If I am not a student, then I do not attend school.

c) Contrapositive: If I do not attend school, then I am not a student.

Equivalences

Alternative Forms of “If p, then q”:

The conditional p → q can be translated in any of the following ways:

1	If p, then q.
2	If p, q.
3	p implies q.
4	p only if q.
5	p is sufficient for q.
6	q is necessary for p.
7	All p are q.
8	q if p.

Example 1: Write each statement in the form “if p, then q.”

You’ll be sorry if I go.

If I go, then you’ll be sorry.

Today is Sunday only if yesterday was Saturday.

If today is Sunday, then yesterday was Saturday.

All Chemists wear lab coats.

If you are a Chemist, then you wear a lab coat.

Biconditionals

The compound statement p if and only if q (often abbreviated p iff q) is called a biconditional. It is symbolized p ↔ q and is interpreted as the conjunction of the two conditionals p → q and q → p.
p ↔ q ≡ (p → q) ⋀ (q → p)

p q	p → q	q → p	(p → q) ⋀ (q → p)
T T	T	T	T
T F	F	T	F
F T	T	F	F
F F	T	T	T

Example 1:

Determine whether each biconditional statement is true or false.

a) 5 + 4 = 9 if and only if 4 + 2 = 6.

True (both component statements are true)

b) 8 = 7 if and only if 8 = 3 + 5.

False (one component is true, one false)

c) 9 + 6 = 12 if and only if 9 + 7 = 10.

True (both component statements are false)

Consistent or Contrary

Two statements about the same object are:

Consistent–if they can both be true.
Contrary–if they both cannot be true.

Example 1:

Consistent–if they can both be true.

That book is nonfiction. That book costs more than $70.

Contrary–if they both cannot be true.

Elvis is alive. Elvis is dead.

Seyeon