[Disc-Math] C.7 Counting Methods and Probability

Date: 2023.06.30 Updated: 2023.06.30

Categories: Disc-Math

Tags: Probability Counting

📋 This is my note-taking from what I learned in the class “Math185-002 Discrete Mathematics”

Overview of Course

Topics

Counting Problems using Not and Or
Discrete Probability- Basic Concepts

Weekly Learning Outcomes

Solve counting problems involving “not” and “or”
Calculate probability using the theoretical and empirical formula.

10.5 Counting Problems using Not and Or

Counting Problems using Not and Or

Set Theory-Logic-Arithmetic Correspondences

	Set Theory	Logic	Arithmetic
Operation or Connective (symbol)	Complement(‘)	Not(~)	Subtraction(-)
Operation or Connective (symbol)	Union(U)	Or(V)	Addition(+)

Problems Involving “NOT”

Suppose U is the set of all possible results of some type. Let A be the set of all those results that satisfy a given condition. The figure below suggests that:

Complements Principle of Counting

The number of ways a certain condition can be satisfied is the total number of possible results minus the number of ways the condition would not be satisfied.

Symbolically, if A is any set within the universal set U, then

n(A) = n(U) - n(A’)

Some events and its complements (NOT)

n(A)	n(A’)
At least one	None
At least two	Less than two = zero OR one
At least three	Less than three = zero OR one OR two
At least n	Less than n

Example 1:

Three friends are boarding a plane. There are only 7 seats left, two of which are window seats. How many ways can the three friends arrange themselves in available seats so that at least one of them gets the window seat?

Solution:

The total number of ways three friends can arrange themselves among 7 seats → n(U) = ₇P₃ = 210

The number of ways to arrange three people among five non-window seats → n(A’) = ₅P₃ = 60

By complements principle we get the following → n(A) = n(U) - n(A’) = 210 - 60 = 150

Example 2: Counting the Proper Subsets of a Set

For the set S = {c, a, l, u, t, o, r}, find the number of proper subsets.

Solution:

A proper subset has less than seven elements. Subsets of many sizes would satisfy this condition. It is easier to consider the one subset that is not proper, namely S itself. S has a total of 2⁷ = 128 subsets. From the complements principle, the number of proper subsets is 128 - 1 = 127.

Example 3: Counting Coin-Tossing Results

If five fair coins are tossed, in how many ways can at least one tail be obtained?

Solution:

By the fundamental counting principle, there are 2⁵ = 32 different results possible. Exactly one of these fails to satisfy “at least one tail.” So from the complements principle, we have the answer: 32 - 1 = 31.

Problems Involving “Or” - Additive Principle of Counting

The number of ways that one or the other of two conditions could be satisfied is the number of ways one of them could be satisfied plus the number of ways the other could be satisfied minus the number of ways they could both be satisfied together.

If A and B are any two sets, then	If A and B are disjoint (n(A∩B)=0, A and B are disjoint), then
n(A∪B) = n(A) + n(B) - n(A∩B)	n(A∪B) = n(A) + n(B)

Example 1:

If you toss eight fair coins, in how many ways can you obtain at least two heads?

Solution:

For each coin there are 2 outcomes (H or T) and we have total eight coins. So total number of outcomes are n(U) = 2⁸ = 256. Complement of “at least two heads” is less than two heads and is equivalent to 0 head OR 1 head.

This involves both the complements principle and additive principle:

Number of ways to obtain at least two heads: n(U) - n(A∪B) = n(U) - [n(A) + n(B)] = 256 - [1+8] = 247

Note: tossing n fair coins and getting m heads/tails = _nC_r

Example 2:

How many five-card hands consist of all hearts or all black cards?

Solution:

n(all heart or all black cards) = n(all hearts) + n(all black cards) = ₁₃C₅ + ₂₆C₅ = 1287 + 65780 = 67067

Example 3: Counting Three-Digit Numbers with Conditions

How many three-digit counting numbers are multiples of 2 or multiples of 5?

Solution:

There are 9(10)(5) = 450 three-digit multiples of 2. A multiple of 5 ends in a 0 or 5, so there are 9(10)(2) 180 of those. A multiple of 2 and 5 must end in a 0. There are 9(10)(1) = 90 of those. So we have 450 + 180 - 90 = 540 three-digit counting numbers that are multiples of 2 or 5.

Example 4: Counting Card-Drawing Results

A single card is drawn from a standard 52-card deck.

a) In how many ways could it be a club or a queen?

b) In how many ways could it be a red card or a face card?

Solution:

a) n(Club OR Queen) = n(Club) + n(Queen) - n(Club ∩ Queen) = ₁₃C₁ + ₄C₁ - ₁C₁ = 13 + 4 - 1 = 16

b) n(Red OR Face) = n(Red) + n(Face) - n(Red ∩ Face) = ₂₆C₁ + ₁₂C₁ - ₆C₁ = 26 + 12 - 6 = 32

11.1 Discrete Probability - Basic Concepts

Discrete Probability - Basic Concepts

Definitions - 1

The study of probability is concerned with random phenomena. Even though we can not be certain whether a given result will occur, we often can obtain a good measure of its likelihood, or probability.
In the study of probability, any observation, or measurement, of a random phenomenon is an experiment.
The possible results of the experiment are called outcomes, and the set of all possible outcomes is called the sample space S.

Example 1:

Tossing three fair coins gives the following eight outcomes. What is sample space?

Solution:

Outcomes: hhh, hht, hth, htt, thh, tht, tth, ttt

Sample space: S = {hhh, hht, hth, htt, thh, tht, tth, ttt}

Definitions - 2

An event is any collection of results or outcomes of an experiment
Outcome that belongs to the event are favorable outcome or success
Equally likely events are events that have the same likelihood of occurring

Example 1:

Event = {htt, tht, tth}

Tossing three coins and getting one head is an event

Tossing three coins and getting exactly one head is a favorable outcome or success

When the die is tossed, each numeral on a die is equally likely to occur

Theoretical (mathematical) Probability Formula

If all outcomes in a finite sample space S are equally likely, and E is an event within that sample space, then the theoretical probability of the event E is given by the formula below. This formula is often referred to as the classical definition of probability.

p(E) = \({number of favorable outcomes(or success)} \over {total number of outcomes}\)
p(E) = \({n(E)} \over {n(S)}\)

Example 1: Finding Probability When Tossing a Coin

If a single fair coin is tossed, find the probability that it will land heads up.

Solution:

The sample space S = {h,t}, and the event whose probability we seek it E = {h}.

P(heads) = P(E) = \({1} \over {2}\)

Outcomes - Rolling 2 Dice

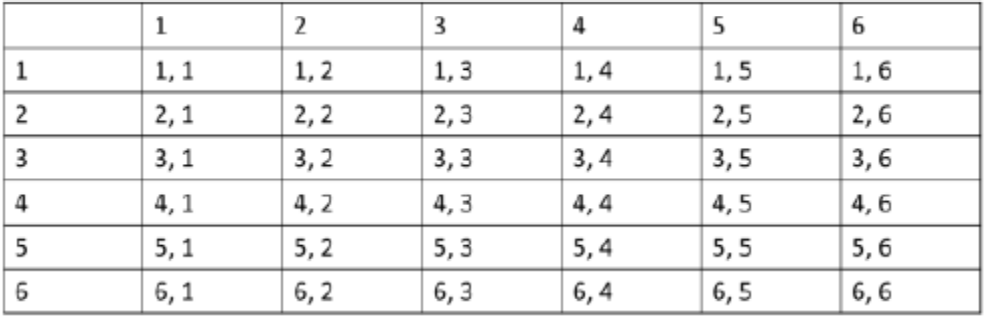
Example 1:

When rolling two dices, what is the probability that the sum is 7?

Solution:

Total outcomes are 36.

Favorable outcomes = {(1,6), (2,5), (3,4), (4,3), (5,2), (6,1)}

P(sum = 7) = 6/36 = 1/6

Example 2: Flipping a Cup

A cup is flipped 100 times. It lands on its side 84 times, on its bottom 6 times, and on its top 10 times. Find the probability that it will land on its top.

Solution:

From the experiment, it appears that P(top) = 10/100 = 1/10

Note: This is an example of experimental or empirical probability.

Empirical Probability Formula

If E is an event that may happen when an experiment is performed, then the empirical probability of event E is given by:

P(E) = \({number of times event E occurred} \over {number of times the experiment was performed}\)

Example 1:

A survey of 880 adults reveals that 85% of them are non-smokers. If one person is randomly selected, find the probability that the selected person is:

a) A smoker:

P(smoker) = \({15\% of 880} \over {880}\) = \({132} \over {880}\) = 0.15

b) A non-smoker:

P(non-smoker) = 1 - 0.15 = 0.85

Example 2:

There are 2,598,960 possible hands in poker. If there are 36 possible ways to have a straight flush, find the probability of being dealt a straight flush.

Solution:

P(straight flush) = \({36} \over {2,598,960}\) ≈ 0.0000139

Example 3:

A school has 820 male students and 835 female students. If a student from the school is selected at random, what is the probability that the student would be a female?

Solution:

P(female) = \({number of female students} \over {total number of students}\) = \({835} \over {820 + 835}\) ≈ 0.505

The Law of Large Numbers

As an experiment is repeated more and more times, the proportion of outcomes favorable to any particular event will tend to come closer and closer to the theoretical probability of that event.

Consider the following demonstration of the law of large numbers. Note that the P(tail) observed is approaching the theoretical probability of 0.5, assuming of course that the coin is “fair”.

Number of Tosses	Number of Tails	P(tails) observed
10	7	0.70
20	11	0.55
100	48	0.48
1000	488	0.488

Odds

If all outcomes in a sample space are equally likely, a of them are favorable to the event E, and the remaining b outcomes are unfavorable to E, then the odds in favor of E are a to b, and the odds against E are b to a.

Example 1: Finding the Odds of Winning a TV

200 tickets were sold for a drawing to win a new television. If Matt purchased 10 of the tickets, what are the odds in favor of Matt’s winning the television?

Solution:

Matt has 10 chances to win and 190 chances to lose. The odds in favor of winning are 10 to 190, or 1 to 19.

Comparison Chart

Basis for Comparison	Odds	Probability
Meaning	Odds refers to the chances in favor of the event to the chances against it.	Probability refers to the likelihood of occurrence of an event.
Expressed in	Ratio	Percent or decimal
Lies between	0 to ∞	0 to 1
Formula	Occurrence/Non-occurrence	Occurrence/Whole

Converting between Probability and Odds

Let E be an event:

If P(E) = \({a} \over {n}\) , then the odds in favor of E are a to (n - a)
If the odds in favor of E are a to b, then P(E) = \({a} \over {a + b}\)
Odds in favor of E = \({P(E)} \over {P(E')}\)
Odds in against of E = \({P(E')} \over {P(E)}\)

Example 1:

If a die rolled once, find the odds in favor of rolling 4.

a) The odds in favor of rolling 4 = \({number of favorable outcomes} \over {number of unfavorable outcomes}\) = \({1} \over {5}\) or 1 to 5

b) The odds against rolling 4 = \({number of unfavorable outcomes} \over {number of favorable outcomes}\) = \({5} \over {1}\) or 5 to 1

Example 2: Converting from Probability to Odds

Suppose the probability of rain today is 43%. Give this information in terms of odds.

Solution:

We can say that P(rain) = 0.43 = 43/100. 43 out of 100 outcomes are favorable, so 100 - 43 = 57 are unfavorable. The odds in favor of rain are 43 to 57 and the odds against rain are 57 to 43.

Example 3: Converting from Odds to Probability

Your odds of completing a College Algebra class are 16 to 9. What is the probability that you will complete the class?

Solution:

There are 16 favorable outcomes and 9 unfavorable. This gives 25 possible outcomes. So, P(completion) = \({16} \over {25}\) = 0.64.

Remarks

a) n coins are tosses (or a coin is tosses n times), total number of outcomes are 2^m.
b) n coins are tosses (or a coin is tosses n times) and getting m heads (or tails) is _nC_r

Seyeon