[Disc-Math] C.2 Set Theory
Categories: Disc-Math
Tags: Set
📋 This is my note-taking from what I learned in the class “Math185-002 Discrete Mathematics”
Overview of Course
Topics
- Venn Diagrams and Subsets
- Set Operations
- Cardinal Numbers and Surveys & Mathematical Systems and Number Theory
Weekly Learning Outcomes
- Find the complement, intersection, union, and difference of sets.
- Find subsets and proper subsets.
- Represent sets with Venn diagrams.
- Fill in a Venn diagrams using cardinal numbers
2.2 Venn Diagrams and Subsets
Venn Diagrams and Subsets
Set
A collection of distinct objects. Each member of the set is called element of the set.
Sets are designated using the following three methods:
- Word description,For Example: The set of even counting numbers less than 10
- The listing method, For Example: {2, 4, 6, 8}
- Set-builder notation, For Example: {x|x is an even counting number less than 10}
Note that:
- Sets are denoted by capital letters.
- Empty set or null set is the set with no element and is denoted by ∅ or { }
- ∈ : is a symbol that reads as “ ELEMENT”,
- ∉ : is a symbol that reads as “NOT AN ELEMENT”
Example 1:
- A = {x|x is odd counting number less than 10}
- A = {1,3,5,7,9}
- 5 ∈ A, 5 is an element of set A
- 6 ∉ A , is not an element of set A
Empty set
The set containing no elements is called the empty set, or null set. The symbol ∅ is used to denote the empty set, so ∅ and { } have the same meaning. We do not denote the empty set with the symbol {∅} because this notation represents a set with one element.
Subsets
1. Subset:
Set A is subset of set B if every element of A is also an element of B. Symbolically A ⊆ B
Example 1:
If A = {a,b,c} and B = {c,b,a}, then A ⊆ B
Example 2:
Write ⊆ or ⊈ in each blank to make a true statement.
- {3,4,5,6} ? {3,4,5,6,8} → Therefore, {3,4,5,6} ⊆ {3,4,5,6,8}
- {1,2,6} ? {2,4,6,8} → Therefore, {1,2,6} ⊈ {2,4,6,8}
- {5,6,7,8} ? {6,5,8,7} → Therefore, {5,6,7,8} ⊆ {6,5,8,7}
2. Proper Subsets:
Set A is a proper subset of B if A ⊆ B and 𝐴 ≠ 𝐵. Symbolically A ⊂ B
Example 1:
If A = {a,b,c} and B = {a,b,c,d}, then A ⊂ B
Example 2:
Decide whether ⊆, ⊂, or both could be placed in each blank to make a true statement.
- {5,6,7} ? {5,6,7,8} → Therefore, {5,6,7} ⊂ {5,6,7,8}
- {a,b,c} ? {a,b,c} → Therefore, {a,b,c} ⊆ {a,b,c}
Set equality
Set A = B if and only if A ⊆ B and B ⊆ A
Example 1:
If A = {1,2,3} and B = {3,1,2}, then A ⊆ B and B ⊆ A, therefore A = B
Number of Subsets
1. Number of Subsets
The number of subsets of a set is given by 2n where n is the cardinal number.
2. Number of Proper Subsets
The number of proper subsets of a set is given by 2n − 1 where n is the cardinal number.
Example 1:
Find the number of subsets and proper subsets of A= {w,x,y,z}
- Number of subsets: 24 = 16
- Number of proper subsets: 24 - 1 = 15
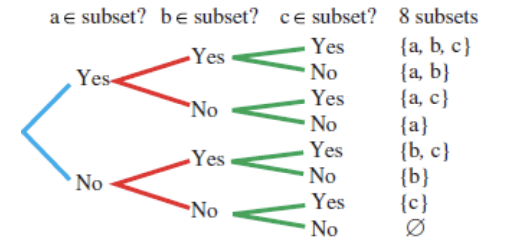
Example 2:
Find all possible subsets of a set {a,b,c} by trial and error.
Here, trial and error leads to eight subsets for {a,b,c}: ∅ , {a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}.
An alternative method involves drawing a tree diagram
- Number of subsets: 23 = 8
- Number of proper subsets: 23 - 1 = 7
Universal Set
The set containing all objects or elements and of which all other sets are subsets. The symbol U is used to denote the universal set.
The Complement of a Set A
The set of elements of U that are not elements of A. Symbolically A’ = {x|x ∈ U and x ∉ A}
Example 1:
Find each set a)M’ b)N’
Let U = {a,b,c,d,e,f,g,h}, M = {a,b,e,f}, and N = {b,d,e,g,h}.
- a) M’ = {c,d,g,h}
- b) N’ = {a,c,f}
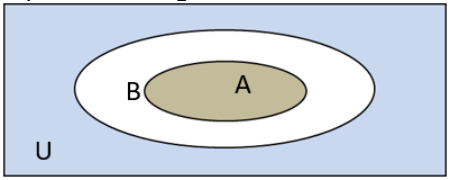
Venn Diagram
Venn diagram of universal set U is represented by the rectangle and any subset A of U is represented by an oval. The region inside U and outside the oval represents A’.
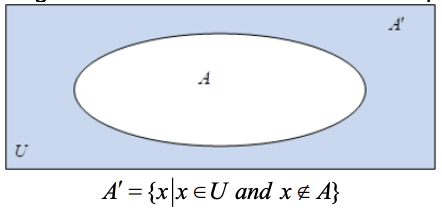
Example 1:
Let U = {1,2,3,4,5,6,7,8}, A = {2,3,5,6}
- What is: A’, the complement of A? Therefore A’ = {1, 4, 7, 8}
- What is U’, the complement of U? Therefore U’ = ∅
- What is ∅’, the complement of ∅? Therefore ∅’ = U
Example 2:
If U = {a,b,c,…,z}, A = {a,b,c}, and B = {a,b,c,d}, then A ⊂ B
Venn diagram for A ⊂ B is depicted in the figure below.
2.3 Set Operations
Set Operations
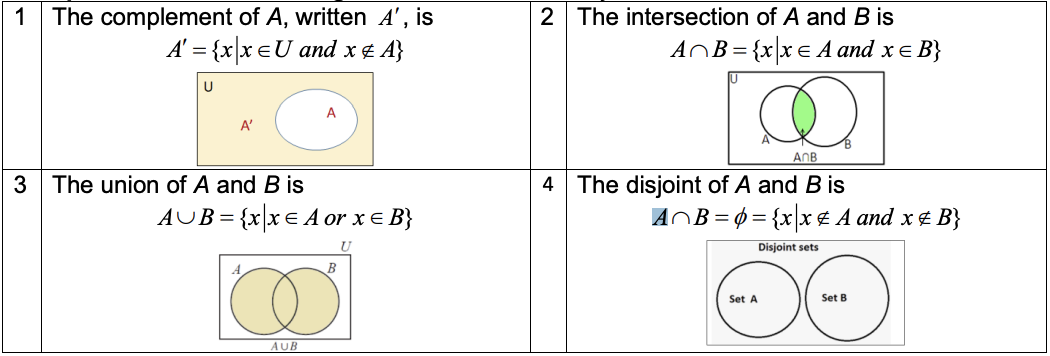
Intersection of Sets
The set of common elements. Symbolically A ∩ B = {x|x ∈ A and x ∈ B}
Example 1:
For sets A = {1,2,3,4,5,6} and B = {4,6,8,10}, then A ∩ B = {4,6}
Union of Sets
The set of all elements belonging to either of the sets. Symbolically A ∪ B = {x|x ∈ A or x ∈ B}
Example 1:
For sets A = {1,2,3,4,5,6} and B = {4,6,8,10}, then A ∪ B = {1,2,3,4,5,6,8,10}
Example 2: Describing Sets in Words
Describe each set in words
- A ∩ (B ∪ C’) → This set might be described as “the set of all elements that are in A, and also are in B or not in C.”
- (A’ ∪ C’) ∩ B’ → One possibility is “the set of all elements that are not in A or not in C, and also are not in B.”
Disjoint Sets
Two sets which have no elements in common. So that A ∩ B = ∅
Example 1:
For sets A = {1,2,3} and B = {4,6,8}, then A ∩ B = ∅
Difference of Sets A and B
Difference of Sets A and B is the set of all elements belonging to set A and not to set B. Symbolically A - B
A - B = {x|x ∈ A and x ∉ B} OR A - B = {x|x ∈ A and x ∈ B’}
Example 1:
For sets A = {1,2,3,4,5,6} and B = {4,6,8,10}, then A - B = {1,2,3,5}
- In general, A - B ≠ B - A
- A - B can also be represented by A ∩ B’
Ordered Pair
A group of two objects designed as first and second components.
In the ordered pair (a,b):
- a is termed the first component.
- b is termed the second component. In the ordered pair (a,b), a is called the first component and b is called the second component.
(a,b) ≠ (b,a) but {a,b} = {b,a}
- Ordered pairs are represented by the parentheses (,)
- In general, (a,b) ≠ (b,a). i.e. order is important!
- Two ordered pairs (a,b) and (c,d) are equal if and only a = c and b = d.
- Sets can contain ordered pairs: {(a,b), (c,d), …}
Cartesian Product of Sets
A set of ordered pairs in which each element of one set can be paired with each element of B. Symbolically A x B
A x B = {(a,b)|a ∈ A and b ∈ B}
Example 1:
Find the Cartesian product of A x B and B x A if A = {a,b,c} and B = {p,q}. What are the similarities/differences between the two resulting sets?
- The Cartesian product of A x B = {(a,p), (a,q), (b,p), (b,q), (c,p), (c,q)}
- The Cartesian product of B x A = {(p,a), (p,b), (p,c), (q,a), (q,b), (q,c)}
Therefore the number of order pairs in the set are same but the order pairs are different in both A x B and B x A.
Cardinal Number of a Cartesian Product
For any two sets A and B, if n(A) = a and n(B) = b, then n(A x B) = n(B x A) = n(A) x n(B) = ab
Example 1:
If n(A) = 3 and n(B) = 2, then n(A x B) = n(B x A) = n(A) x n(B) = 3 x 2 = 6
De Morgan’s Laws
For any two sets A and B, (A ∩ B)’ = A’ ∪ B’ and (A ∪ B)’ = A’ ∩ B’
Set Operations and Venn Diagram
Let A and B be any sets within a universal set U.
Fundamental Set Properties

Symbols Used in Set Notation
| Notation | Name | Meaning |
|---|---|---|
| A ∪ B | Union | Elements that belong to set A or set B or both A and B |
| A ∩ B | Intersection | Elements that belong to both set A and set B |
| A ⊆ B | Subset | Every element of set A is also in set B |
| A ⊂ B | Proper Subset | Every element of A is also in B, but B contains more elements |
| A ⊄ B | Not a Subset | Elements of set A are not elements of set B |
| A = B | Equal Sets | Both set A and B have the same elements |
| Ac or A’ | Complement | Elements not in set A but in the universal set |
| A - B or A\B | Set Difference | Elements in set A but not in set B |
| P(A) | Power Set | The set of all subsets of set A |
| A x B | Cartesian Product | The set that contains all the ordered pairs from set A and B in that order |
| n(A) or |A| | Cardinality | The number of elements in set A |
| ∅ or { } | Empty Set | The set that has no elements |
| U | Universal Set | The set that contains all the elements under consideration |
2.4 Surveys and Cardinal Numbers
Surveys and Cardinal Numbers
Cardinal Number Formula
For any two sets A and B, n(A ∪ B) = n(A) + n(B) − n(A ∩ B)
Example 1:
Find n(A) if n(A ∪ B) = 22, n(A ∩ B) = 8, and n(B) = 12. We solve the cardinal number formula for n(A).
n(A) = n(A ∪ B) − n(B) + n(A ∩ B) = 22 − 12 + 8 = 18
Example 2:
Find n(B) if n(A ∪ B) = 30, n(A ∩ B) = 10, and n(A) = 18 We solve the cardinal number formula for n(A).
n(B) = n(A ∪ B) − n(A) + n(A ∩ B) = 30 − 10 + 18 = 38
Example 3:
Use the numerals representing cardinalities in the Venn diagrams to give the cardinality of each set specified.
Example 4:
Find n(A) if n(A ∪ B) = 55, n(A ∩ B) = 15, and n(B) = 35. We solve the cardinal number formula for n(A).
n(A) = n(A ∪ B) − n(B) + n(A ∩ B) = 55 − 35 + 15 = 35
Example 5:
Find n(A∪B) if n(B) = 28, n(A∩B) = 5, and n(A) = 16. We solve the cardinal number formula for n(A).
n(A ∪ B) = n(A) + n(B) − n(A ∩ B) = 16 + 28 − 5 = 39
Example 6:
Draw a Venn diagram and use the given information to fill in the number of elements in each region.
n(A) = 19, n(B) = 13, n(A ∪ B) = 25, n(A’) = 11
Solution:
Example 7: Use Venn diagrams
Joe Long worked on 9 music projects last year.
- He wrote and produced 3 projects.
- He wrote a total of 5 projects.
- He produced a total of 7 projects.
- (a) How many projects did he write but not produce?
- (b) How many projects did he produce but not write?
Solution:
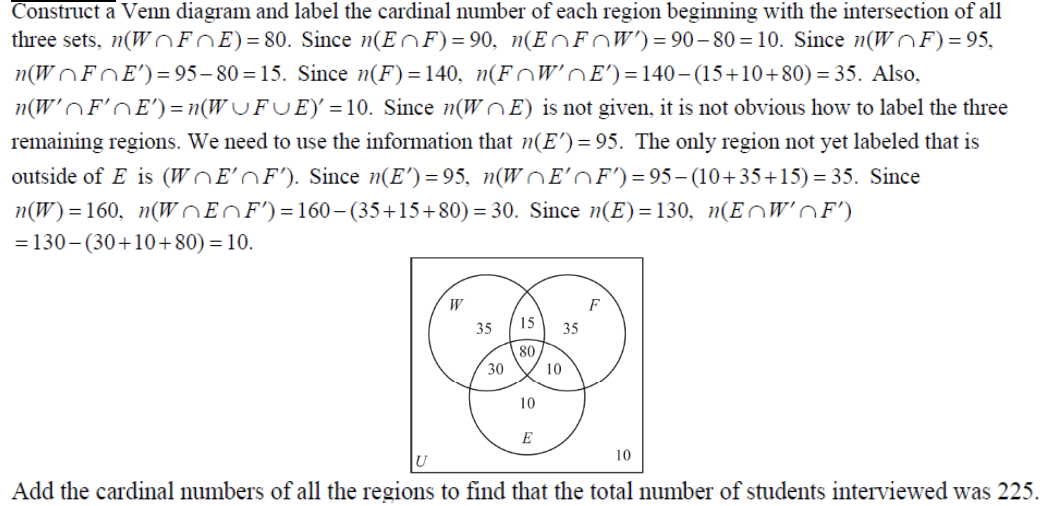
Example 8:
Sofia, who sells college textbooks, interviewed first-year students on a community college campus to find out the main goals of today’s students.
- Let W = the set of those who want to be wealthy,
- F = the set of those who want to raise a family,
- E = the set of those who want to become experts in their fields.
Sofia’s findings are summarized here.
- n(W) = 160
- n(F) = 140
- n(E) = 130
- n(W ∩ F) = 95
- n(E ∩ F) = 90
- n(W ∩ F ∩ E) = 80
- n(E’) = 95
- n[(W ∪ F ∪ E)’] = 10
Find the total number of students interviewed.
Solution:
Example 9: Use Venn diagram
Gitti is a fan of the music of Paul Simon and Art Garfunkel. In her collection of 25 compact discs, she has the following:
- 5 on which both Simon and Garfunkel sing
- 7 on which Simon sings
- 8 on which Garfunkel sings
- 15 on which neither Simon nor Garfunkel sings.
- (a) How many of her compact discs feature only Paul Simon?
- (b) How many of her compact discs feature only Art Garfunkel?
- (c) How many feature at least one of these two artists?
- (d) How many feature at most one of these two artists?
Solution:
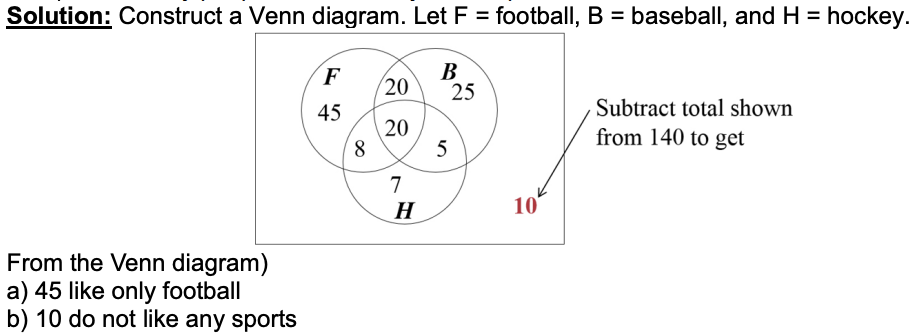
Example 10: Analyzing a Survey
Suppose that a group of 140 people were questioned about particular sports that they watch regularly and the following information was produced.
- 93 like football
- 70 like baseball
- 40 like hockey
- 40 like football and baseball
- 25 like baseball and hockey
- 28 like football and hockey
- 20 like all three
- a) How many people like only football?
- b) How many people don’t like any of the sports?
Solution:


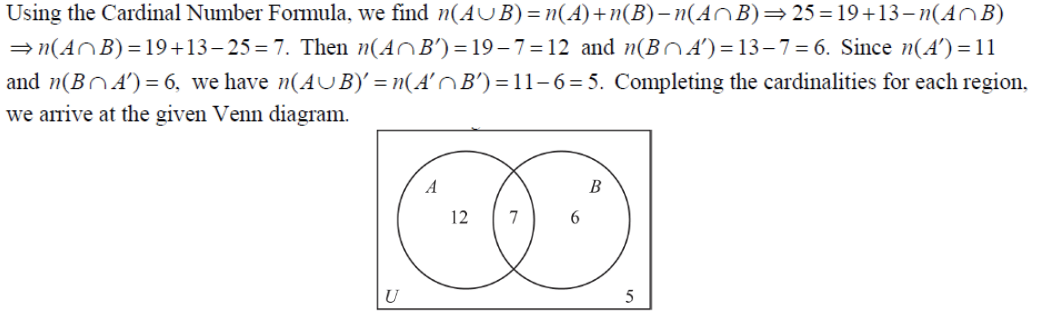


Leave a comment